---

Problem 107

---

Minimal Network

The following undirected network consists of seven vertices and twelve edges with a total weight of $243$.

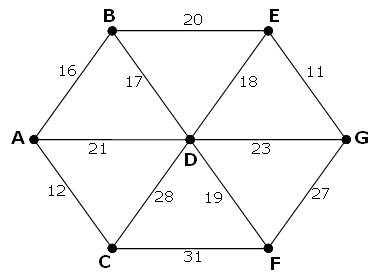
The same network can be represented by the matrix below.

	$A$	$B$	$C$	$D$	$E$	$F$	$G$
$A$	-	16	12	21	-	-	-
$B$	16	-	-	17	20	-	-
$C$	12	-	-	28	-	31	-
$D$	21	17	28	-	18	19	23
$E$	-	20	-	18	-	-	11
$F$	-	-	31	19	-	-	27
$G$	-	-	-	23	11	27	-

However, it is possible to optimise the network by removing some edges and still ensure that all points on the network remain connected. The network which achieves the maximum saving is shown below. It has a weight of $93$, representing a saving of $243-93=150$ from the original network.

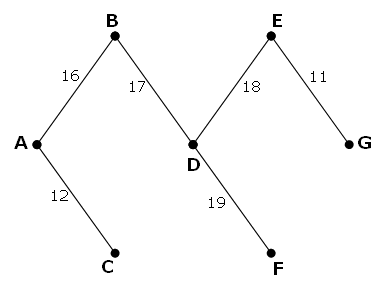
Using network.txt (right click and ‘Save Link/Target As…’), a 6K text file containing a network with forty vertices, and given in matrix form, find the maximum saving which can be achieved by removing redundant edges whilst ensuring that the network remains connected.

---

最小网络

如下图所示的无向网络包含有$7$个顶点和$12$条边，其总权重为$243$。

这个网络也可以表示为如下的邻接矩阵形式：

	$A$	$B$	$C$	$D$	$E$	$F$	$G$
$A$	-	16	12	21	-	-	-
$B$	16	-	-	17	20	-	-
$C$	12	-	-	28	-	31	-
$D$	21	17	28	-	18	19	23
$E$	-	20	-	18	-	-	11
$F$	-	-	31	19	-	-	27
$G$	-	-	-	23	11	27	-

不过，我们其实可以优化这个网络，移除其中的一些边，同时仍然保证每个顶点之间都是连通的。节省的权重最多的新网络如下图所示，其总权重为$93$，相比原网络节省了$243-93=150$的权重。

文本文件network.txt中包含了一个有四十个顶点的网络的邻接矩阵表示。移除其中冗余的边，同时仍然保证每个顶点之间都是连通的，并求出最多能节省多少权重。

---