Problem 109
Darts
In the game of darts a player throws three darts at a target board which is split into twenty equal sized sections numbered one to twenty.
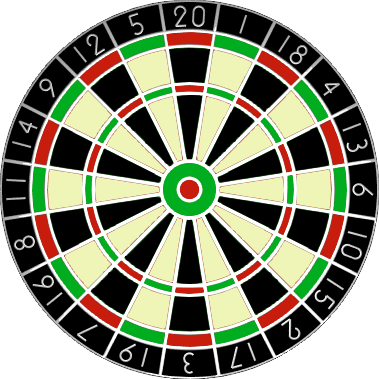
The score of a dart is determined by the number of the region that the dart lands in. A dart landing outside the red/green outer ring scores zero. The black and cream regions inside this ring represent single scores. However, the red/green outer ring and middle ring score double and treble scores respectively.
At the centre of the board are two concentric circles called the bull region, or bulls-eye. The outer bull is worth $25$ points and the inner bull is a double, worth $50$ points.
There are many variations of rules but in the most popular game the players will begin with a score $301$ or $501$ and the first player to reduce their running total to zero is a winner. However, it is normal to play a “doubles out” system, which means that the player must land a double (including the double bulls-eye at the centre of the board) on their final dart to win; any other dart that would reduce their running total to one or lower means the score for that set of three darts is “bust”.
When a player is able to finish on their current score it is called a “checkout” and the highest checkout is $170$: $T20$ $T20$ $D25$ (two treble $20$s and double bull).
There are exactly eleven distinct ways to checkout on a score of $6$:
| $D3$ | ||
| $D1$ | $D2$ | |
| $S2$ | $D2$ | |
| $D2$ | $D1$ | |
| $S4$ | $D1$ | |
| $S1$ | $S1$ | $D2$ |
| $S1$ | $T1$ | $D1$ |
| $S1$ | $S3$ | $D1$ |
| $D1$ | $D1$ | $D1$ |
| $D1$ | $S2$ | $D1$ |
| $S2$ | $S2$ | $D1$ |
Note that $D1$ $D2$ is considered different to $D2$ $D1$ as they finish on different doubles. However, the combination $S1$ $T1$ $D1$ is considered the same as $T1$ $S1$ $D1$.
In addition we shall not include misses in considering combinations; for example, $D3$ is the same as $0$ $D3$ and $0$ $0$ $D3$.
Incredibly there are $42336$ distinct ways of checking out in total.
How many distinct ways can a player checkout with a score less than $100$?
飞镖
在飞镖游戏中,玩家每一轮需向靶子上投掷三枚飞镖;靶子被分成了二十个相等面积的区域,并分别标上$1$至$20$作为基础分值。

每一枚飞镖的分数还取决于它的位置:落在外围的红/绿色圈以外时为零分,落在黑/白色区域时为一倍得分,而落在外围和中间的红/绿色圈时分别为两倍和三倍得分。
在靶子的正中心有两个同心圆,被称为靶心。射中靶心外圈得$25$分,射中靶心内圈则得双倍$50$分。
飞镖的规则有许多变种,但最热门的一种是,每个玩家从$301$分或$501$分开始,轮流投掷飞镖并减去得分,首先将自己的分数减少到恰好为$0$的玩家获胜。不过,通常会采用“双倍结束”规则,即玩家的最后一镖必须射中一个双倍区域(包括双倍的靶心内圈)才能判定获胜。若这一轮的得分使得玩家的分数减少到$1$分或更少,但最后一镖未射中双倍区域,则这一轮的得分“作废”。
玩家在当前分数下能够获胜则被称为“结分”。最高的结分为$170$:$T20$ $T20$ $D25$(两个三倍$20$分和一个双倍靶心)。
当玩家分数为$6$时,恰好有$11$种结分方式:
| $D3$ | ||
| $D1$ | $D2$ | |
| $S2$ | $D2$ | |
| $D2$ | $D1$ | |
| $S4$ | $D1$ | |
| $S1$ | $S1$ | $D2$ |
| $S1$ | $T1$ | $D1$ |
| $S1$ | $S3$ | $D1$ |
| $D1$ | $D1$ | $D1$ |
| $D1$ | $S2$ | $D1$ |
| $S2$ | $S2$ | $D1$ |
注意$D1$ $D2$被认为是不同于$D2$ $D1$的结分方式,因为它们最后的双倍不同。不过,组合$S1$ $T1$ $D1$和$T1$ $S1$ $D1$就被认为是相同的结分方式。
另外,在计算结分方式时,我们不考虑脱靶的情况;例如,$D3$和$0$ $D3$以及$0$ $0$ $D$3就是相同的结分方式。
令人惊奇的是,一共有$42336$种不同的结分方式。
当玩家当前分数小于$100$时,一共有多少种不同的结分方式?