---

Problem 174

---

Counting the number of “hollow” square laminae that can form one, two, three, … distinct arrangements

We shall define a square lamina to be a square outline with a square “hole” so that the shape possesses vertical and horizontal symmetry.

Given eight tiles it is possible to form a lamina in only one way: 3x3 square with a 1x1 hole in the middle. However, using thirty-two tiles it is possible to form two distinct laminae.

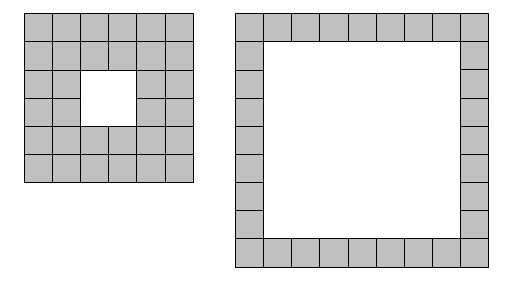
If t represents the number of tiles used, we shall say that t = 8 is type L(1) and t = 32 is type L(2).

Let N(n) be the number of t ≤ 1000000 such that t is type L(n); for example, N(15) = 832.

What is ∑ N(n) for 1 ≤ n ≤ 10?

---

能组成一种、两种、三种……不同方形基板的地砖数计数

我们定义一个方形基板为一个拥有方形外框，中间有一个方形的“洞”且在水平和竖直方向上均对称的图形。

用八块地砖我们只能拼出一种方形基板：一个3x3的方格，正中间有一个1x1的洞。然而，用32块地砖，我们能够拼出两种不同的方形基板。

如果用t代表使用的地砖数，我们称t = 8是L(1)型的，而t = 32是L(2)型的。

记N(n)为满足t ≤ 1000000且为L(n)型的t的个数；例如，N(15) = 832。

对于1 ≤ n ≤ 10，求∑ N(n)。

---