Problem 184
Triangles containing the origin
Consider the set Ir of points (x,y) with integer co-ordinates in the interior of the circle with radius r, centered at the origin, i.e. x2 + y2 < r2.
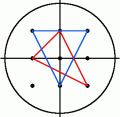
For a radius of 2, I2 contains the nine points (0,0), (1,0), (1,1), (0,1), (-1,1), (-1,0), (-1,-1), (0,-1) and (1,-1). There are eight triangles having all three vertices in I2 which contain the origin in the interior. Two of them are shown below, the others are obtained from these by rotation.
For a radius of 3, there are 360 triangles containing the origin in the interior and having all vertices in I3 and for I5 the number is 10600.
How many triangles are there containing the origin in the interior and having all three vertices in I105?
包含原点的三角形
集合Ir包含了以原点为圆心,半径为r的圆内的所有格点(x,y),也即满足x2 + y2 < r2的点。
若半径为2,I2中包含了9个点(0,0), (1,0), (1,1), (0,1), (-1,1), (-1,0), (-1,-1), (0,-1)和(1,-1)。有八个三角形,其顶点都在I2中,且原点在三角形内部。下图所示是其中的两个,另外那些可以通过旋转这两个三角形得到。

若半径为3,有360个三角形包含原点在其内部且顶点在I3中;对于I5这个数字是10600。
有多少个三角形包含原点在其内部且顶点在I105中?