---

Problem 189

---

Tri-colouring a triangular grid

Consider the following configuration of 64 triangles:

We wish to colour the interior of each triangle with one of three colours: red, green or blue, so that no two neighbouring triangles have the same colour. Such a colouring shall be called valid. Here, two triangles are said to be neighbouring if they share an edge.
Note: if they only share a vertex, then they are not neighbours.

For example, here is a valid colouring of the above grid:

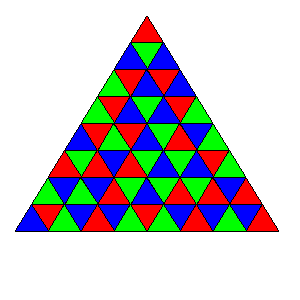
A colouring C’ which is obtained from a colouring C by rotation or reflection is considered distinct from C unless the two are identical.

How many distinct valid colourings are there for the above configuration?

---

三角形阵的三染色

考虑按如下方式摆放的64个三角形：

我们想要给每个三角形的内部染上红、绿、蓝这三种颜色之一，而且任意两个相邻的三角形所染颜色不同，这样的染色方案我们视为有效。在这里，两个相邻的三角形是指它们共用一条边。
注意：共用一个顶点的三角形并不视为相邻三角形。

例如，下图是一个上述三角形阵的有效染色方案：

我们认为可以由染色方案C旋转而成的染色方案C’与C是不同的，除非C旋转后得到的染色方案与其完全一致。

对于上述三角形阵，有多少种不同的有效染色方案？

---