---

Problem 194

---

Coloured Configurations

Consider graphs built with the units A: 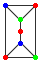and B: 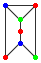, where the units are glued along the vertical edges as in the graph .

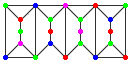A configuration of type (a,b,c) is a graph thus built of a units A and b units B, where the graph’s vertices are coloured using up to c colours, so that no two adjacent vertices have the same colour.
The compound graph above is an example of a configuration of type (2,2,6), in fact of type (2,2,c) for all c ≥ 4.

Let N(a,b,c) be the number of configurations of type (a,b,c).
For example, N(1,0,3) = 24, N(0,2,4) = 92928 and N(2,2,3) = 20736.

Find the last 8 digits of N(25,75,1984).

---

染色摆放方案

考虑由A单元：和B单元组成的图形，相邻单元相互重叠在一起如下图所示。

一个(a,b,c)类型的染色摆放方案，是一个由a个A单元和b个B单元摆放组成，并用至多c种颜色给每个顶点染色并保证相邻顶点所染颜色不同的图形.
上面这个复合图形就是(2,2,6)类型染色摆放方案的一个例子，事实上它也属于任意(2,2,c)类型，只要c ≥ 4即可。

记N(a,b,c)是(a,b,c)类型的染色摆放方案总数。
例如，N(1,0,3) = 24，N(0,2,4) = 92928，以及N(2,2,3) = 20736。

求N(25,75,1984)的最后8位小数。

---