---

Problem 630

---

Crossed lines

Given a set, $L$, of unique lines, let $M(L)$ be the number of lines in the set and let $S(L)$ be the sum over every line of the number of times that line is crossed by another line in the set. For example, two sets of three lines are shown below:

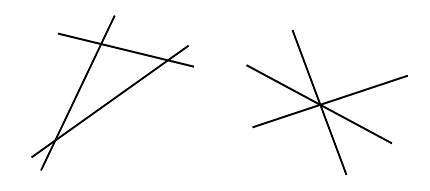
In both cases $M(L)$ is $3$ and $S(L)$ is $6$: each of the three lines is crossed by two other lines. Note that even if the lines cross at a single point, all of the separate crossings of lines are counted.

Consider points $(T_{2k-1},T_{2k})$, for integer $k\ge 1$, generated in the following way:

$S_0=290797$
$S_{n+1}=S^2_n \mod 50515093$
$T_n=(S_n \mod 2000) - 1000$

For example, the first three points are: (527, 144), (−488, 732), (−454, −947). Given the first $n$ points generated in this manner, let $L_n$ be the set of unique lines that can be formed by joining each point with every other point, the lines being extended indefinitely in both directions. We can then define $M(L_n)$ and $S(L_n)$ as described above.

For example, $M(L_3)=3$ and $S(L_3)=6$. Also $M(L_{100})=4948$ and $S(L_{100})=24477690$.

Find $S(L_{2500})$.

---

交叉的直线

给定一系列相异直线的集合$L$，记$M(L)$为集合中直线的数目，而$S(L)$为所有这些直线与集合中其它直线相交的次数之和。例如，考虑下图所示的两组直线集合：

在这两种情形中，$M(L)$均为$3$而$S(L)$均为$6$：每个集合有三条直线，每条直线都与其它两条直线各相交一次。注意到，即使这些直线交于同一点，每次相交也都分别计算。

考虑由以下方式构造的一系列点$(T_{2k-1},T_{2k})$，其中整数$k\ge 1$：

$S_0=290797$
$S_{n+1}=S^2_n \mod 50515093$
$T_n=(S_n \mod 2000) - 1000$

例如，前三个点分别是：(527, 144)，(−488, 732)，(−454, −947)。给定由这种方式给出的前$n$个点，并记$L_n$为将这些点两两连接所得的所有相异直线构成的集合；注意直线总是向两端延长至无限远处。相应地，可以按照上述定义给出$M(L_n)$和$S(L_n)$。

例如，$M(L_3)=3$而$S(L_3)=6$。此外，$M(L_{100})=4948$而$S(L_{100})=24477690$。

求$S(L_{2500})$。

---