---

Problem 638

---

Weighted lattice paths

Let $P_{a.b}$ denote a path in a $a\times b$ lattice grid with following properties:

• The path begins at $(0,0)$ and ends at $(a,b)$.
• The path consists only of unit moves upwards or to the right; that is the coordinates are increasing with every move.

Denote $A(P_{a,b})$ to be the area under the path. For the example of a $P_{4,3}$ path given below, the area equals $6$.

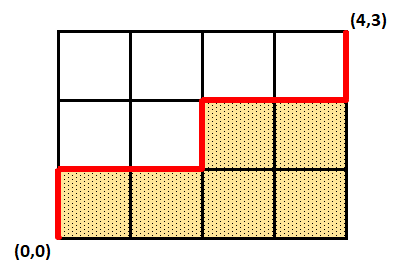
Define $G(P_{a,b},k)=k^{A(P_{a,b})}$. Let $C(a,b,k)$ equal the sum of $G(P_{a,b},k)$ over all valid paths in a $a\times b$ lattice grid.

You are given that

• $C(2,2,1)=6$
• $C(2,2,2)=6$
• $C(10,10,1)=184756$
• $C(15,10,3)\equiv 880419838\mathrm{mod}1000000007$
• $C(10000,10000,4)\equiv 395913804\mathrm{mod}1000000007$

Calculate $\sum _{k=1}^{7}C({10}^k+k,{10}^k+k,k)$. Give your answer modulo $1000000007$.

---

带权格阵路径

记$P_{a.b}$为$a\times b$格阵中满足如下性质的路径：

• 路径从$(0,0)$开始，到$(a,b)$结束。
• 路径只能沿着格阵每次向上或向右走一步；也就是说，每一步都只能使横、纵坐标增加而不能减少。

记$A(P_{a,b})$为路径下方区域的面积。以下图给出的一条$P_{4,3}$路径为例，其下方区域的面积为$6$。

记$G(P_{a,b},k)=k^{A(P_{a,b})}$。记 $C(a,b,k)$为$a\times b$格阵中所有满足上述条件的路径所对应的$G(P_{a,b},k)$之和。

已知

• $C(2,2,1)=6$
• $C(2,2,2)=6$
• $C(10,10,1)=184756$
• $C(15,10,3)\equiv 880419838\mathrm{mod}1000000007$
• $C(10000,10000,4)\equiv 395913804\mathrm{mod}1000000007$

求$\sum _{k=1}^{7}C({10}^k+k,{10}^k+k,k)$，并将答案对$1000000007$取余。

---