Problem 644

Squares on the line

Sam and Tom are trying a game of (partially) covering a given line segment of length $L$ by taking turns in placing unit squares onto the line segment.

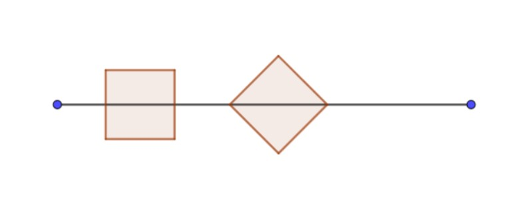
As illustrated below, the squares may be positioned in two different ways, either “straight” by placing the midpoints of two opposite sides on the line segment, or “diagonal” by placing two opposite corners on the line segment. Newly placed squares may touch other squares, but are not allowed to overlap any other square laid down before.
The player who is able to place the last unit square onto the line segment wins.

With Sam starting each game by placing the first square, they quickly realise that Sam can easily win every time by placing the first square in the middle of the line segment, making the game boring.

Therefore they decide to randomise Sam’s first move, by first tossing a fair coin to determine whether the square will be placed straight or diagonal onto the line segment and then choosing the actual position on the line segment randomly with all possible positions being equally likely. Sam’s gain of the game is defined to be $0$ if he loses the game and $L$ if he wins. Assuming optimal play of both players after Sam’s initial move, you can see that Sam’s expected gain, called $e (L)$ , is only dependent on the length of the line segment.

For example, if $L = 2$ , Sam will win with a probability of $1$ , so $e (2) = 2$ .
Choosing $L = 4$ , the winning probability will be $0.33333333$ for the straight case and $0.22654092$ for the diagonal case, leading to $e (4) = 1.11974851$ (rounded to $8$ digits after the decimal point each).

Being interested in the optimal value of $L$ for Sam, let’s define $f (a, b)$ to be the maximum of $e (L)$ for some $L \in [a, b]$ .
You are given $f (2, 10) = 2.61969775$ , being reached for $L = 7.82842712$ , and $f (10, 20) = 5.99374121$ (rounded to $8$ digits each).

Find $f (200, 500)$ , rounded to $8$ digits after the decimal point.

线段的正方形覆盖

山姆和汤姆正在玩一个游戏：在一条长为 $L$ 的线段上，他们轮流摆放单位正方形，以（部分地）覆盖这个线段。

如下图所示，有两种摆放正方形的方式，一种是“横放”，将正方形两条对边的中点放在线段上，另一种是“斜放”，将正方形沿对角线放在线段上。后放的正方形可以与先放的正方形接触，但是不允许重叠。
如果在一名玩家摆放完正方形之后，对方无法再摆放新的正方形，则前者获胜。

一开始，总是由山姆先摆放正方形，但他们很快发现，山姆只需把第一个正方形摆放在线段正中间，就必定能够获胜，这样的游戏太无聊了。

于是他们决定，山姆必须随机摆放第一个正方形：先抛掷一枚公平硬币，决定这个正方形是横放还是斜放，然后再在线段上等概率地选择正方形摆放的位置。双方约定，如果山姆输了，那么他的收益为 $0$ ，反之他的收益为 $L$ 。在摆完第一个正方形之后，如果双方都采用最优策略，可以看出山姆的期望收益 $e (L)$ 只取决于线段的长度。

例如，如果 $L = 2$ ，山姆必定获胜，所以 $e (2) = 2$ 。
如果 $L = 4$ ，当第一个正方形横放时，山姆获胜的概率是 $0.33333333$ ，而斜放时概率是 $0.22654092$ ，因此 $e (4) = 1.11974851$ （均保留小数点后 $8$ 位小数）。

我们希望知道，在一定范围内，对山姆来说最优的线段长度 $L$ 应该是多少，因此我们记 $f (a, b)$ 为所有 $L \in [a, b]$ 对应的 $e (L)$ 中的最大值。
已知 $f (2, 10) = 2.61969775$ ，此时最优长度为 $L = 7.82842712$ ；我们还知道 $f (10, 20) = 5.99374121$ （均保留小数点后 $8$ 位小数）。

求 $f (200, 500)$ ，并保留小数点后 $8$ 位小数。