---

Problem 662

---

Fibonacci paths

Alice walks on a lattice grid. She can step from one lattice point $A (a,b)$ to another $B (a+x,b+y)$ providing distance $AB = \sqrt{x^2+y^2}$ is a Fibonacci number ${1,2,3,5,8,13,\ldots}$ and $x\ge 0,$ $y\ge 0$.

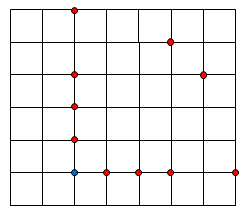
In the lattice grid below Alice can step from the blue point to any of the red points.

Let $F(W,H)$ be the number of paths Alice can take from $(0,0)$ to $(W,H)$.
You are given $F(3,4) = 278$ and $F(10,10) = 215846462$.

Find $F(10,000,10,000) \bmod 1,000,000,007$.

---

斐波那契路径

爱丽丝正在格阵上行走，每次她都可以从一个格点$A (a,b)$走到另一个格点$B (a+x,b+y)$，只要两点间距离$AB = \sqrt{x^2+y^2}$是一个斐波那契数${1,2,3,5,8,13,\ldots}$，且$x\ge 0$，$y\ge 0$。

如下图的格阵，从蓝点出发，爱丽丝可以前往任意一个红点。

记$F(W,H)$为爱丽丝从$(0,0)$出发到达$(W,H)$的可行路径数目。
已知，$F(3,4) = 278$，$F(10,10) = 215846462$。

求$F(10,000,10,000) \bmod 1,000,000,007$.

---