Problem 664

An infinite game

Peter is playing a solitaire game on an infinite checkerboard, each square of which can hold an unlimited number of tokens.

Each move of the game consists of the following steps:

Choose one token $T$ to move. This may be any token on the board, as long as not all of its four adjacent squares are empty.
Select and discard one token $D$ from a square adjacent to that of $T$ .
Move $T$ to any one of its four adjacent squares (even if that square is already occupied).

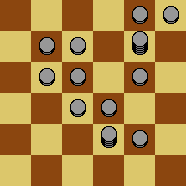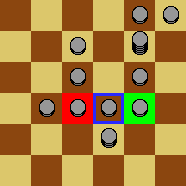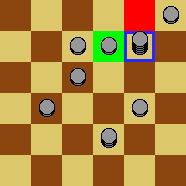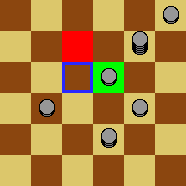
The board is marked with a line called the dividing line. Initially, every square to the left of the dividing line contains a token, and every square to the right of the dividing line is empty:

Peter’s goal is to get a token as far as possible to the right in a finite number of moves. However, he quickly finds out that, even with his infinite supply of tokens, he cannot move a token more than four squares beyond the dividing line.

Peter then considers starting configurations with larger supplies of tokens: each square in the $d$ th column to the left of the dividing line starts with $d^{n}$ tokens instead of $1$ . This is illustrated below for $n = 1$ :

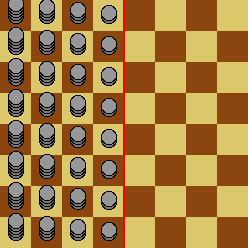
Let $F (n)$ be the maximum number of squares Peter can move a token beyond the dividing line. For example, $F (0) = 4$ . You are also given that $F (1) = 6$ , $F (2) = 9$ , $F (3) = 13$ , $F (11) = 58$ and $F (123) = 1173$ .

Find $F (1234567)$ .

无限游戏

彼得在玩一个单人游戏，这个游戏需要一张无穷大的棋盘，棋盘上的每一格都可以放置无限枚棋子。

游戏中的每次行动由以下几个步骤构成：

选择一枚棋子 $T$ ，这枚棋子的四个相邻方格不能全部为空。
从与 $T$ 相邻的方格中选择并移除一枚棋子 $D$ 。
将 $T$ 移动至四个相邻方格之一（棋子可以堆叠）。

棋盘上画有一条竖直线，称为分割线。游戏开始时，在分割线左侧的每一格中放上一枚棋子，而分割线右侧的每一格置空。

彼得的目标是，在有限步内，将一枚棋子移动到分割线右侧尽可能远处。然而，他很快发现，即使他有无限枚棋子，他也只能将一枚棋子向右移动至多四格。

于是彼得转而考虑增加初始局面下棋子的数目：在从分割线向左数第 $d$ 列的所有格子中，一开始放上 $d^{n}$ 枚而不是 $1$ 枚棋子。如下图所示为 $n = 1$ 时的初始局面：

记 $F (n)$ 为此时彼得能够移动棋子到达的最远距离。例如， $F (0) = 4$ 。已知 $F (1) = 6$ ， $F (2) = 9$ ， $F (3) = 13$ ， $F (11) = 58$ ， $F (123) = 1173$ 。

求 $F (1234567)$ 。