Problem 671

Colouring a Loop

A certain type of tile comes in three different sizes - $1\times 1$, $1\times2$, and $1\times 3$ - and in $k$ different colours. There is an unlimited number of tiles available in each combination of size and colour.

These are used to tile a closed loop of width $2$ and length (circumference) $n$, where $n$ is a positive integer, subject to the following conditions:

The loop must be fully covered by non-overlapping tiles.
It is not permitted for four tiles to have their corners meeting at a single point.
Adjacent tiles must be of different colours.

For example, the following is an acceptable tiling of a $2\times 23$ loop with $k=4$ (blue, green, red and yellow):

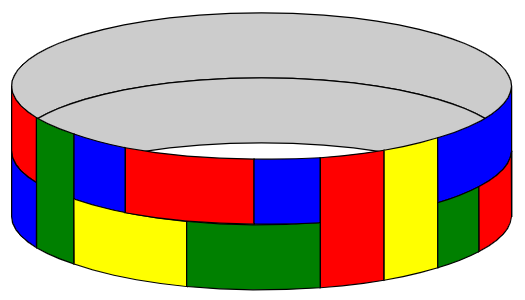
but the following is not an acceptable tiling, because it violates the “no four corners meeting at a point” rule:

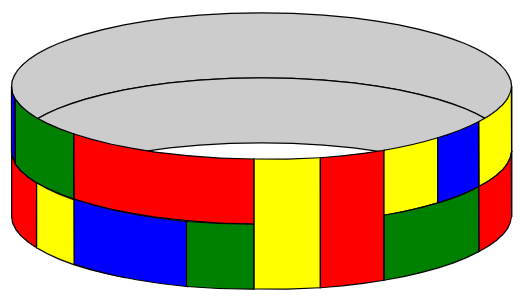
Let $F_k(n)$ be the number of ways the $2\times n$ loop can be tiled subject to these rules when $k$ colours are available. (Not all $k$ colours have to be used.) Where reflecting horizontally or vertically would give a different tiling, these tilings are to be counted separately.

For example, $F_4(3) = 104$, $F_5(7) = 3327300$, and $F_6(101)\equiv 75309980 \pmod{1,000,004,321}$.

Find $F_{10}(10,004,003,002,001) \bmod 1,000,004,321$.

彩砖环形铺盖

某种砖块有三种不同的大小，分别是$1\times 1$、$1\times2$和$1\times 3$，同时又有$k$种不同的颜色。每种大小和颜色组合的砖块都不限量供应。

这些砖块被用于铺盖宽度为$2$、长度（周长）为$n$的圆环，其中$n$为正整数。铺盖过程必须满足以下条件：

圆环必须完全被覆盖，且砖块之间不能重叠。
不允许有四块砖块共用一个顶点。
相邻的砖块必须有不同的颜色。

例如，下图是$k=4$（分别是蓝色、绿色、红色和黄色）时对大小为$2\times 23$的圆环的一种合理铺盖：

而下图则是一种不合理铺盖，因为这种铺盖违背了“四块砖块不允许共用一个顶点”的规则：

记$F_k(n)$为有$k$种颜色时，大小为$2\times n$的圆环上的合理铺盖总数。（$k$种颜色不必全都用上。）上下或左右镜像对称的铺盖视为不同的铺盖。

已知，$F_4(3) = 104$，$F_5(7) = 3327300$，$F_6(101)\equiv 75309980 \pmod{1,000,004,321}$。

求$F_{10}(10,004,003,002,001) \bmod 1,000,004,321$。