---

Problem 726

---

Falling bottles

Consider a stack of bottles of wine. There are $n$ layers in the stack with the top layer containing only one bottle and the bottom layer containing $n$ bottles. For $n=4$ the stack looks like the picture below.

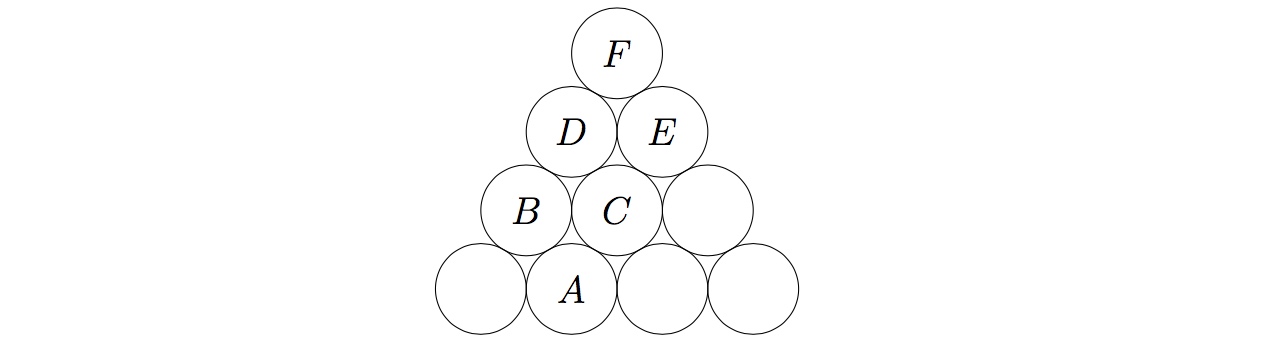
The collapsing process happens every time a bottle is taken. A space is created in the stack and that space is filled according to the following recursive steps:

• No bottle touching from above: nothing happens. For example, taking $F$.
• One bottle touching from above: that will drop down to fill the space creating another space. For example, taking $D$.
• Two bottles touching from above: one will drop down to fill the space creating another space. For example, taking $C$.

This process happens recursively; for example, taking bottle $A$ in the diagram above. Its place can be filled with either $B$ or $C$. If it is filled with $C$ then the space that $C$ creates can be filled with $D$ or $E$. So there are $3$ different collapsing processes that can happen if $A$ is taken, although the final shape (in this case) is the same.

Define $f(n)$ to be the number of ways that we can take all the bottles from a stack with $n$ layers. Two ways are considered different if at any step we took a different bottle or the collapsing process went differently.

You are given $f(1)=1$, $f(2)=6$ and $f(3)=1008$.

Also define
$${\displaystyle S(n)=\sum _{k=1}^{n}f(k)}$$

Find $S({10}^4)$ and give your answer modulo $1000000033$.

---

掉落的酒瓶

一堆酒瓶被摆成$n$层，其中最顶层只有一个酒瓶，而最底层有$n$个酒瓶。如下图所示为$n=4$时酒瓶的摆放示例。

每次从这堆酒瓶中拿走一瓶酒，就会触发一连串掉落过程。被拿走的酒瓶所留下的空位会根据以下规则填满：

• 空位上方没有酒瓶，则什么都不会发生，比如在上图中拿走$F$。
• 空位上方只有一个酒瓶，则该酒瓶掉落填补空位，并在原位置留下一个新的空位，比如在上图中拿走$D$。
• 空位上方有两个酒瓶，则其中一个酒瓶掉落填补空位，并在原位置留下一个新的空位，比如在上图中拿走$C$。

如果有新空位出现，则上述过程会持续进行；例如，在上图中拿走$A$，所留下的空位可以被$B$或$C$填补。若$C$填补了该空位，则$C$留下的新空位可以被$D$或$E$填补。因此，拿走$A$之后总共有$3$种不同的掉落过程，尽管它们最终导致的酒堆形状是相同的。

记$f(n)$为从$n$层酒堆中拿走所有瓶子的不同方式，这里的不同既指在每一步拿走的酒瓶的不同，也指拿走酒瓶后的掉落过程的不同。

已知$f(1)=1$，$f(2)=6$，$f(3)=1008$。

再记
$${\displaystyle S(n)=\sum _{k=1}^{n}f(k)}$$

求$S({10}^4)$，并将你的答案对$1000000033$取余。

---