Problem 807

Loops of Ropes

Given a circle $C$ and an integer $n > 1$ , we perform the following operations.

In step $0$ , we choose two uniformly random points $R_{0}$ and $B_{0}$ on $C$ .

In step $i$ ( $1 \leq i < n$ ), we first choose a uniformly random point $R_{i}$ on $C$ and connect the points $R_{i - 1}$ and $R_{i}$ with a red rope; then choose a uniformly random point $B_{i}$ on $C$ and connect the points $B_{i - 1}$ and $B_{i}$ with a blue rope.

In step $n$ , we first connect the points $R_{n - 1}$ and $R_{0}$ with a red rope; then connect the points $B_{n - 1}$ and $B_{0}$ with a blue rope.

Each rope is straight between its two end points, and lies above all previous ropes.

After step $n$ , we get a loop of red ropes, and a loop of blue ropes.

Sometimes the two loops can be separated, as in the left figure below; sometimes they are “linked”, hence cannot be separated, as in the middle and right figures below.

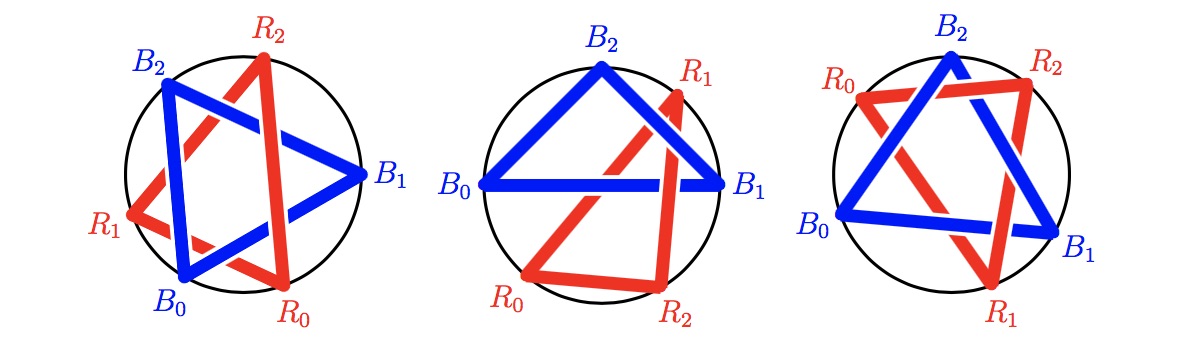
Let $P (n)$ be the probability that the two loops can be separated.

For example, $P (3) = \frac{11}{20}$ and $P (5) \approx 0.4304177690$ .

Find $P (80)$ , rounded to $10$ digits after decimal point.

绳环

考虑圆 $C$ 和整数 $n > 1$ ，我们进行如下操作。

在第 $0$ 步，我们在圆 $C$ 上均匀随机地选择两个点 $R_{0}$ 和 $B_{0}$ 。

在第 $i$ 步( $1 \leq i < n$ ），我们先在圆 $C$ 上均匀随机地选择一个点 $R_{i}$ 并将点 $R_{i - 1}$ 和点 $R_{i}$ 用红绳连接，再在圆 $C$ 上均匀随机地选择一个点 $B_{i}$ ，并将点 $B_{i - 1}$ 和点 $B_{i}$ 用蓝绳连接。

在第 $n$ 步，我们先将点 $R_{n - 1}$ 和点 $R_{0}$ 用红绳连接，再将点 $B_{n - 1}$ 和点 $B_{0}$ 用蓝绳连接。

每条绳在其连接的端点之间都是直线，且都位于所有现有绳的上方。

在完成第 $n$ 步之后，我们得到了一个红绳环和一个蓝绳环。

有时这两个绳环可以拆开，如下图左所示。有时这两个绳环相互缠绕，无法拆开，如下图中和下图右所示。

记 $P (n)$ 为两个绳环可以拆开的概率。

例如， $P (3) = \frac{11}{20}$ ， $P (5) \approx 0.4304177690$ 。

求 $P (80)$ ，并将你的答案保留小数点后 $10$ 位。