Problem 84
Monopoly Odds
In the game, Monopoly, the standard board is set up in the following way:
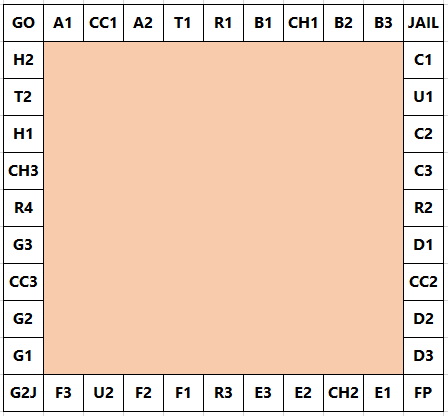
A player starts on the GO square and adds the scores on two $6$-sided dice to determine the number of squares they advance in a clockwise direction. Without any further rules we would expect to visit each square with equal probability: $2.5\%$. However, landing on G2J (Go To Jail), CC (community chest), and CH (chance) changes this distribution.
In addition to G2J, and one card from each of CC and CH, that orders the player to go directly to jail, if a player rolls three consecutive doubles, they do not advance the result of their $3$rd roll. Instead they proceed directly to jail.
At the beginning of the game, the CC and CH cards are shuffled. When a player lands on CC or CH they take a card from the top of the respective pile and, after following the instructions, it is returned to the bottom of the pile. There are sixteen cards in each pile, but for the purpose of this problem we are only concerned with cards that order a movement; any instruction not concerned with movement will be ignored and the player will remain on the CC/CH square.
- Community Chest ($2/16$ cards):
- Advance to GO
- Go to JAIL
- Chance ($10/16$ cards)
- Advance to GO
- Go to JAIL
- Go to C1
- Go to E3
- Go to H2
- Go to R1
- Go to next R (railway company)
- Go to next R
- Go to next U (utility company)
- Go back $3$ squares
The heart of this problem concerns the likelihood of visiting a particular square. That is, the probability of finishing at that square after a roll. For this reason it should be clear that, with the exception of G2J for which the probability of finishing on it is zero, the CH squares will have the lowest probabilities, as $5/8$ request a movement to another square, and it is the final square that the player finishes at on each roll that we are interested in. We shall make no distinction between “Just Visiting” and being sent to JAIL, and we shall also ignore the rule about requiring a double to “get out of jail”, assuming that they pay to get out on their next turn.
By starting at GO and numbering the squares sequentially from $00$ to $39$ we can concatenate these two-digit numbers to produce strings that correspond with sets of squares.
Statistically it can be shown that the three most popular squares, in order, are JAIL ($6.24\%$) = Square $10$, E3 ($3.18\%$) = Square $24$, and GO ($3.09\%$) = Square $00$. So these three most popular squares can be listed with the six-digit modal string: $102400$.
If, instead of using two $6$-sided dice, two $4$-sided dice are used, find the six-digit modal string.
大富翁几率
大富翁游戏的标准棋盘大致如下图所示:

玩家从起点GO出发,掷两个六面的骰子并将点数和相加,作为本轮前进的步数。如果没有其它规则,那么落在每一格上的概率应该是$2.5\%$。但是,由于G2J(入狱)、CC(宝箱卡)和CH(机会卡)的存在,这个分布会有所改变。
除了落在G2J上,或者在CC或CH上抽到入狱卡之外,如果玩家连续三次都掷出两个相同的点数,则在第三次时将会直接入狱。
游戏开始时,宝箱卡和机会卡将被洗牌打乱。当一个玩家落在CC或CH上时,他们从宝箱卡和机会卡的牌堆最上方取一张卡,遵循指令行动,并将该卡放回牌堆的最下方。宝箱卡和机会卡都各有$16$张,但我们只关心会移动位置的卡片,其它的卡片我们都将无视它们的效果。
- 宝箱卡 ($2/16$ 张卡):
- 回到起点GO
- 进入监狱JAIL
- 机会卡 ($10/16$ 张卡):
- 回到起点GO
- 进入监狱JAIL
- 移动到C1
- 移动到E3
- 移动到H2
- 移动到R1
- 移动到下一个R(铁路公司)
- 移动到下一个R
- 移动到下一个U(公共服务公司)
- 后退三步
这道题主要考察掷出骰子后停在某个特定方格上的概率。显然,除了停在G2J上的可能性为$0$之外,停在CH格的可能性最小,因为有$5/8$的情况下玩家会移动到另一格。我们不区分是被送进监狱还是恰好移动到监狱这一格,而且不考虑需要掷出两个相同的点数才能出狱的要求,而是假定进入监狱的第二轮就会自动出狱。
从起点GO开始,将方格依次标记$00$到$39$,我们就可以将这些两位数连接起来表示方格的序列。
统计学上来说,三个最有可能停下的方格分别是JAIL($6.24\%$)或方格$10$,E3($3.18\%$)或方格$24$,以及GO($3.09\%$)或方格$00$。这三个方格可以用一个六位数字串表示:$102400$。
假设我们不用两个六面的骰子,而是用两个四面的骰子进行游戏,求出三个最有可能停下的方格所构成的六位数字串。