Problem 842

Irregular Star Polygons

Given $n$ equally spaced points on a circle, we define an $n$-star polygon as an $n$-gon having those $n$ points as vertices. Two $n$-star polygons differing by a rotation/reflection are considered different.

For example, there are twelve $5$-star polygons shown below.

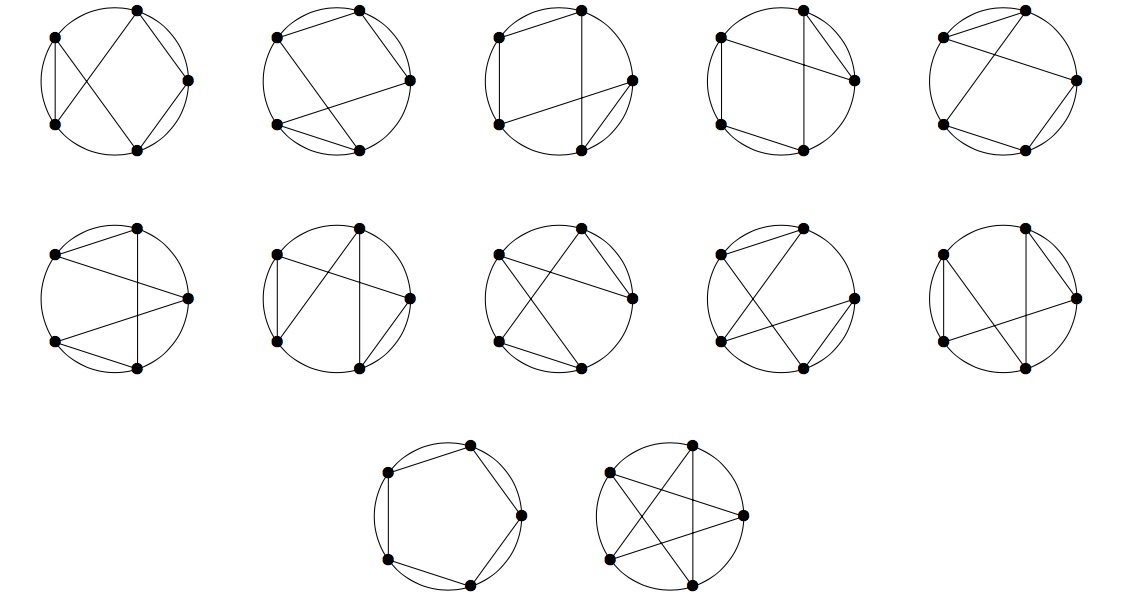
For an $n$-star polygon $S$, let $I(S)$ be the number of its self intersection points.

Let $T(n)$ be the sum of $I(S)$ over all $n$-star polygons $S$.

For the example above $T(5) = 20$ because in total there are $20$ self intersection points.

Some star polygons may have intersection points made from more than two lines. These are only counted once. For example, $S$, shown below is one of the sixty $6$-star polygons. This one has $I(S) = 4$.

You are also given that $T(8) = 14640$.

Find $\displaystyle \sum_{n = 3}^{60}T(n)$. Give your answer modulo $(10^9 + 7)$.

不规则星形多边形

在圆上取$n$个等距离的点，称以这$n$个点为顶点的$n$边形为$n$星多边形。若两个$n$星多边形可以通过旋转或翻折重合，仍视为不同的$n$星多边形。

例如，共有十二个不同的$5$星多边形，如下图所示：

对于任意$n$星多边形$S$，记$I(S)$为其各边自交产生的交点数目。

记$T(n)$为所有$n$星多边形$S$对应的$I(S)$之和。

如上图所示，$T(5) = 20$，因为所有$5$星多边形各边自交共产生$20$个交点。

有些交点可能由多条边同时相交产生，这样的交点只被计算一次。例如，下图所示是六十种$6$星多边形的其中之一，其对应的$I(S)=4$。

已知$T(8) = 14640$。

求$\displaystyle \sum_{n = 3}^{60}T(n)$，并将你的答案对$(10^9 + 7)$取余。