Problem 846
Magic Bracelets
A bracelet is made by connecting at least three numbered beads in a circle. Each bead can only display $1$, $2$, or any number of the form $p^k$ or $2p^k$ for odd prime $p$.
In addition a magic bracelet must satisfy the following two conditions:
- no two beads display the same number
- the product of the numbers of any two adjacent beads is of the form $x^2+1$
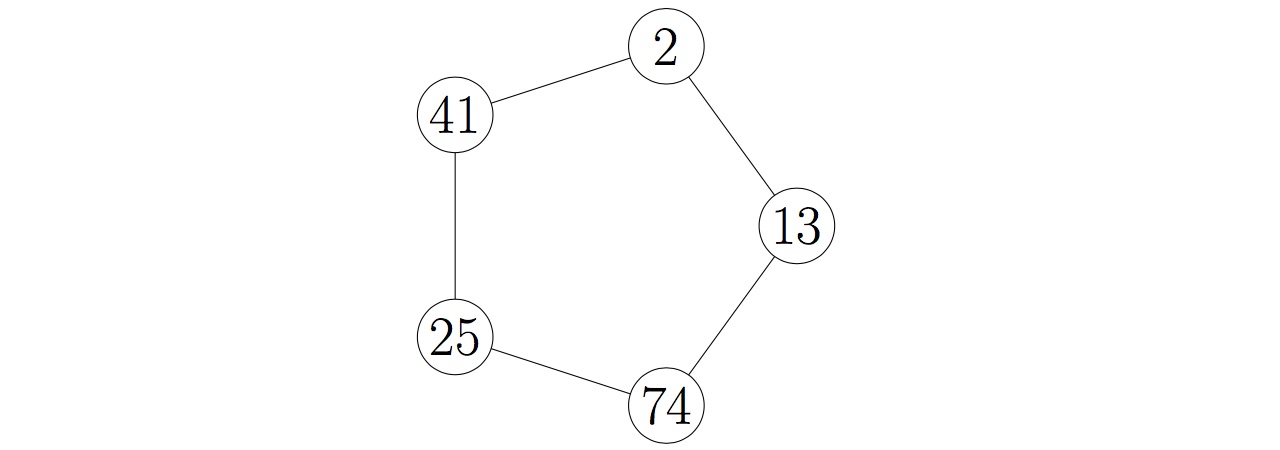
Define the potency of a magic bracelet to be the sum of numbers on its beads.
The example is a magic bracelet with five beads which has a potency of $155$.
Let $F(N)$ be the sum of the potency of each magic bracelet which can be formed using positive integers not exceeding $N$, where rotations and reflections of an arrangement are considered equivalent. You are given $F(20)=258$ and $F(10^2)=538768$.
Find $F(10^6)$.
魔法手镯
将至少三颗有编号的珠子穿成一圈就构成了手镯。每颗珠子的编号只能是$1$、$2$或任何形如$p^k$或$2p^k$的整数且满足$p$为奇素数。
魔法手镯则必须额外满足以下两个条件:
- 任意两颗珠子的编号都不同
- 两颗相邻珠子的编号的乘积可以写成$x^2+1$的形式

记魔法手镯的效力为其所有珠子的编号之和。
如上图所示是一枚有五颗珠子、效力为$155$的魔法手镯。
记$F(N)$为所有由编号不超过$N$的珠子串成的魔法手镯的效力之和,其中经旋转或翻折可以重合的编号方案视为等价的方案。已知$F(20)=258$,$F(10^2)=538768$。
求$F(10^6)$。