Problem 86

Cuboid route

A spider, S, sits in one corner of a cuboid room, measuring $6$ by $5$ by $3$, and a fly, F, sits in the opposite corner. By travelling on the surfaces of the room the shortest “straight line” distance from S to F is $10$ and the path is shown on the diagram.

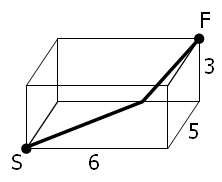
However, there are up to three “shortest” path candidates for any given cuboid and the shortest route doesn’t always have integer length.

It can be shown that there are exactly $2060$ distinct cuboids, ignoring rotations, with integer dimensions, up to a maximum size of $M$ by $M$ by $M$, for which the shortest route has integer length when $M = 100$. This is the least value of $M$ for which the number of solutions first exceeds two thousand; the number of solutions when $M = 99$ is $1975$.

Find the least value of $M$ such that the number of solutions first exceeds one million.

长方体路径

蜘蛛S位于一个大小为$6 \times 5 \times 3$的长方体房间的一角，而苍蝇F则恰好位于其对角。沿着房间的墙面，从S到F的最短“直线”距离是$10$，路径如下图所示：

对于任意长方体房间，对角顶点间的“最短”路径总是有三种可能的方案；此外，最短路径的长度也并不一定为整数。

当$M=100$时，若不考虑旋转，在所有长、宽、高均不超过$M$且为整数的长方体中，对角顶点之间的最短距离是整数的恰好有$2060$个。$M=100$也是使得满足条件的长方体数目超过两千的最小值：当$M=99$时，该数目为$1975$。

求使得满足条件的长方体数目超过一百万的最小$M$值。