Problem 860

Gold and Silver Coin Game

Gary and Sally play a game using gold and silver coins arranged into a number of vertical stacks, alternating turns. On Gary’s turn he chooses a gold coin and removes it from the game along with any other coins sitting on top. Sally does the same on her turn by removing a silver coin. The first player unable to make a move loses.

An arrangement is called fair if the person moving first, whether it be Gary or Sally, will lose the game if both play optimally.

Define $F (n)$ to be the number of fair arrangements of $n$ stacks, all of size $2$ . Different orderings of the stacks are to be counted separately, so $F (2) = 4$ due to the following four arrangements:

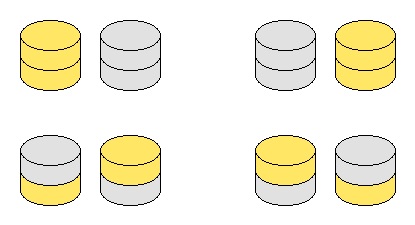
You are also given $F (10) = 63594$ .

Find $F (9898)$ . Give your answer modulo $989898989$ .

金银硬币游戏

盖瑞和萨利在玩一个游戏，游戏开始时有若干堆竖直堆放的金币和银币，两人轮流行动。轮到盖瑞时，他可以任选一枚金币，并将这枚金币和所有堆放在其上方的硬币移出游戏；轮到萨利时则是可以任选一枚银币。首先无法行动的玩家输掉游戏。

如果一个初始局面使得，无论先行玩家是盖瑞还是萨利，他在采取最优策略的情况下都必败，则称之为公平初始局面。

定义 $F (n)$ 为所有包含 $n$ 堆、每堆各 $2$ 枚硬币的公平初始局面的数目。堆的顺序不同时视为不同的初始局面，因此 $F (2) = 4$ ，相应的四种初始局面如下所示：

已知 $F (10) = 63594$ 。

求 $F (9898)$ ，并对 $989898989$ 取余作为你的答案。