---

Problem 91

---

Right triangles with integer coordinates

The points $P(x_1,y_1)$ and $Q(x_2,y_2)$ are plotted at integer co-ordinates and are joined to the origin, $O(0,0)$, to form $\triangle OPQ$.

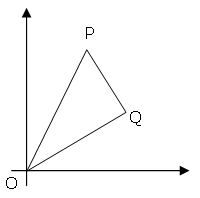
There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between $0$ and $2$ inclusive; that is, $0 \le x_1, y_1, x_2, y_2 \le 2$.

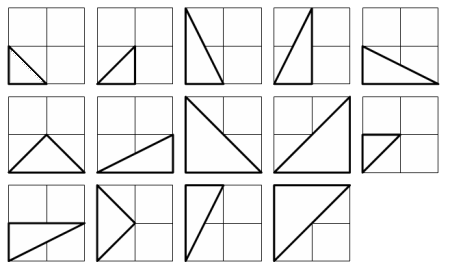
Given that $0 \le x_1, y_1, x_2, y_2 \le 50$, how many right triangles can be formed?

---

格点直角三角形

考虑格点$P(x_1,y_1)$和$Q(x_2,y_2)$与原点$O(0,0)$相连构成的三角形$\triangle OPQ$。

当点$P$和点$Q$的坐标在$0$到$2$之间，也即$0 \le x_1, y_1, x_2, y_2 \le 2$时，恰好能构造出$14$个直角三角形。

若$0 \le x_1, y_1, x_2, y_2 \le 50$，能构造出多少个直角三角形？

---