Problem 919

Fortunate Triangles

We call a triangle fortunate if it has integral sides and at least one of its vertices has the property that the distance from it to the triangle’s orthocentre is exactly half the distance from the same vertex to the triangle’s circumcentre.

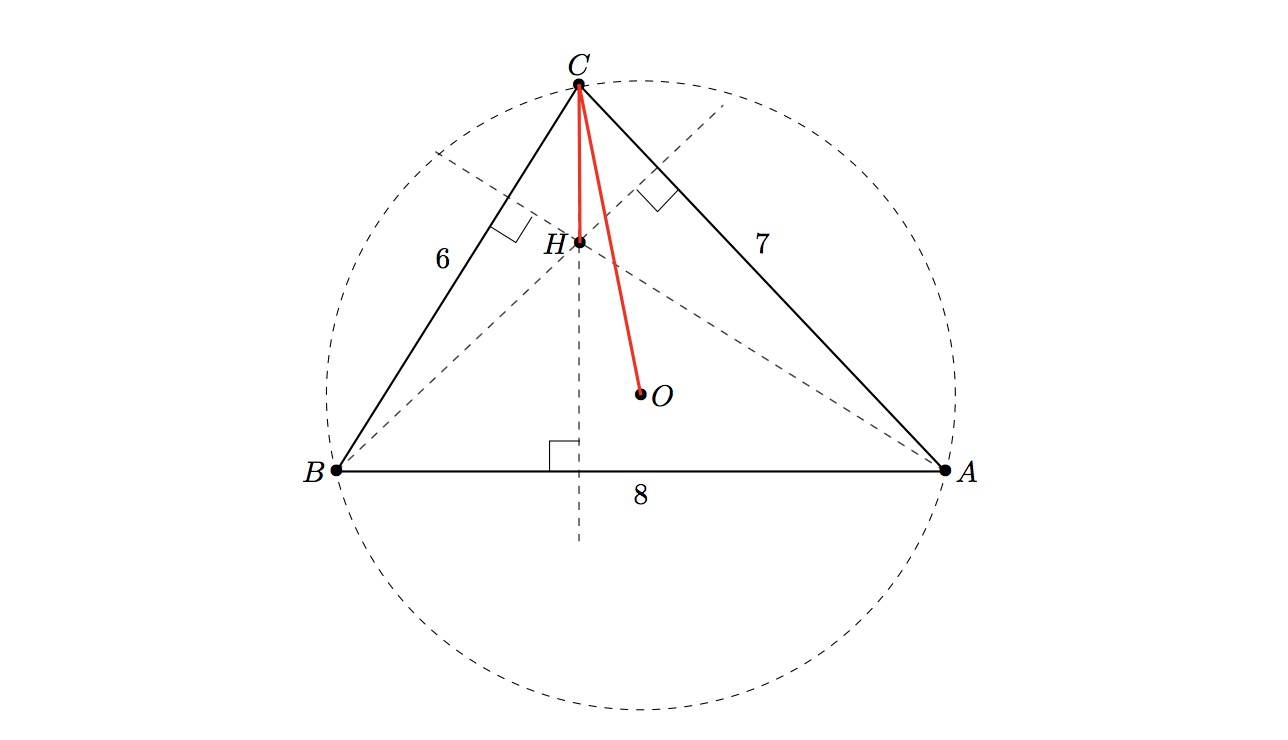
Triangle $A B C$ above is an example of a fortunate triangle with sides $(6, 7, 8)$ . The distance from the vertex $C$ to the circumcentre $O$ is $\approx 4.131182$ , while the distance from $C$ to the orthocentre $H$ is half that, at $\approx 2.065591$ .

Define $S (P)$ to be the sum of $a + b + c$ over all fortunate triangles with sides $a \leq b \leq c$ and perimeter not exceeding $P$ .

For example $S (10) = 24$ , arising from three triangles with sides $(1, 2, 2)$ , $(2, 3, 4)$ , and $(2, 4, 4)$ . You are also given $S (100) = 3331$ .

Find $S (10^{7})$ .

幸运三角形

幸运三角形是指具有整数边长且至少有一个顶点满足以下性质的三角形：该顶点到三角形垂心的距离恰好是同一顶点到三角形外心的距离的一半。

如上图所示的三角形 $A B C$ 就是一个边长为 $(6, 7, 8)$ 的幸运三角形。顶点 $C$ 到外心 $O$ 的距离约为 $\approx 4.131182$ ，而 $C$ 到垂心 $H$ 的距离是其一半，约为 $\approx 2.065591$ 。

定义 $S (P)$ 为所有满足边长 $a \leq b \leq c$ 且周长不超过 $P$ 的幸运三角形的边长和 $a + b + c$ 之和。

例如， $S (10) = 24$ ，对应三个边长分别为 $(1, 2, 2)$ 、 $(2, 3, 4)$ 和 $(2, 4, 4)$ 的三角形。此外还已知 $S (100) = 3331$ 。

求 $S (10^{7})$ 。