---

Problem 923

---

Young’s Game B

A Young diagram is a finite collection of (equally-sized) squares in a grid-like arrangement of rows and columns, such that

• the left-most squares of all rows are aligned vertically;
• the top squares of all columns are aligned horizontally;
• the rows are non-increasing in size as we move top to bottom;
• the columns are non-increasing in size as we move left to right.

Two examples of Young diagrams are shown below.

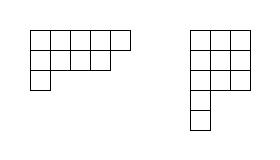
Two players Right and Down play a game on several Young diagrams, all disconnected from each other. Initially, a token is placed in the top-left square of each diagram. Then they take alternating turns, starting with Right. On Right’s turn, Right selects a token on one diagram and moves it one square to the right. On Down’s turn, Down selects a token on one diagram and moves it one square downwards. A player unable to make a legal move on their turn loses the game.

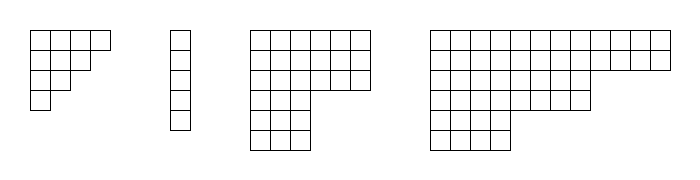
For $a,b,k\ge 1$ we define an $(a,b,k)$-staircase to be the Young diagram where the bottom-right frontier consists of $k$ steps of vertical height $a$ and horizontal length $b$. Shown below are four examples of staircases with $(a,b,k)$ respectively $(1,1,4)$, $(5,1,1)$, $(3,3,2)$, $(2,4,3)$.

Additionally, define the weight of an $(a,b,k)$-staircase to be $a+b+k$.

Let $S(m,w)$ be the number ways of choosing $m$ staircases, each having weight not exceeding $w$, upon which Right (moving first in the game) will win the game assuming optimal play. Different orderings of the same set of staircases are to be counted separately.

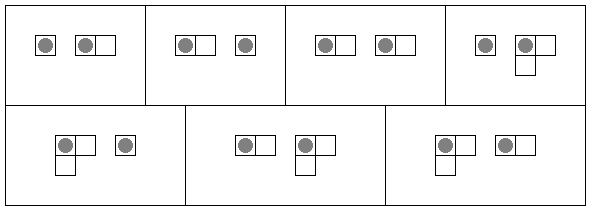
For example, $S(2,4)=7$ is illustrated below, with tokens as grey circles drawn in their initial positions.

You are also given $S(3,9)=315319$.

Find $S(8,64)$ giving your answer modulo ${10}^9+7$.

---

杨氏游戏（二）

杨氏图表是指一类有限个（大小相等的）方格组合，这些方格按照网格状排列成行和列，且满足以下条件：

• 所有行最左边的方格垂直对齐；
• 所有列最上边的方格水平对齐；
• 自上而下，行的宽度单调不增；
• 自左而右，列的高度单调不增。

下图展示了两个杨氏图表的例子。

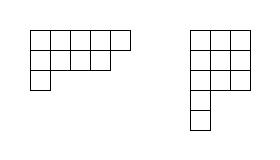
两位玩家阿右和阿下在若干个相互分离的杨氏图表上玩一个游戏。游戏开始时，在每个图表的左上角方格放置一枚棋子。然后他们轮流行动，阿右先行。在阿右的回合，阿右选择一个图表中的棋子并向右移动一格。在阿下的回合，阿下选择一个图表中的棋子并向下移动一格。如果一位玩家在其回合无法进行合法移动，则输掉游戏。

对于$a,b,k\ge 1$，定义$(a,b,k)$-阶梯为满足如下条件的杨氏图表：其右下边界由$k$个台阶组成，每个台阶垂直高度为$a$，水平长度为$b$。下图展示了四个阶梯的例子，它们的$(a,b,k)$值分别为$(1,1,4)$、$(5,1,1)$、$(3,3,2)$、$(2,4,3)$。

另外，定义$(a,b,k)$-阶梯的重量为$a+b+k$。

令$S(m,w)$为选择$m$个阶梯、每个阶梯的重量不超过$w$且在最优操作下阿右（游戏先手方）将获胜的方法数目。相同阶梯集合的不同排列要分别计数。

例如，下图展示了$S(2,4)=7$，其中灰色圆圈表示棋子的初始位置。

已知$S(3,9)=315319$。

求$S(8,64)$，并对${10}^9+7$取余作为你的答案。

---