Problem 927

Prime-ary Tree

A full $k$-ary tree is a tree with a single root node, such that every node is either a leaf or has exactly $k$ ordered children. The height of a $k$-ary tree is the number of edges in the longest path from the root to a leaf.

For instance, there is one full $3$-ary tree of height $0$, one full $3$-ary tree of height $1$, and seven full $3$-ary trees of height $2$. These seven are shown below.

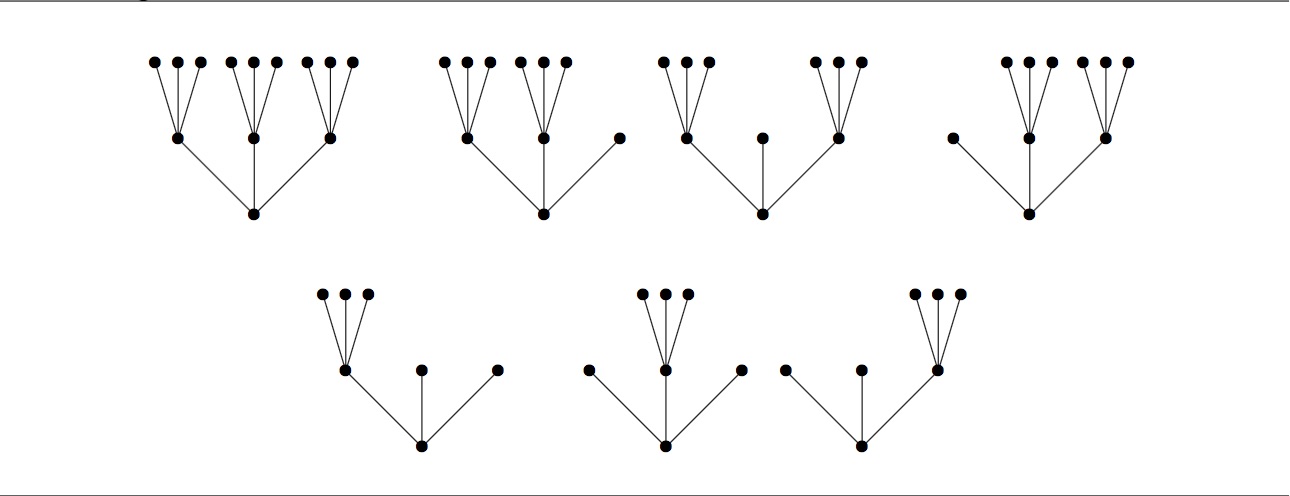
For integers $n$ and $k$ with $n\ge 0$ and $k \ge 2$, define $t_k(n)$ to be the number of full $k$-ary trees of height $n$ or less.

Thus, $t_3(0) = 1$, $t_3(1) = 2$, and $t_3(2) = 9$. Also, $t_2(0) = 1$, $t_2(1) = 2$, and $t_2(2) = 5$.

Define $S_k$ to be the set of positive integers $m$ such that $m$ divides $t_k(n)$ for some integer $n\ge 0$. For instance, the above values show that $1$, $2$, and $5$ are in $S_2$ and $1$, $2$, $3$, and $9$ are in $S_3$.

Let $S = \bigcap_p S_p$ where the intersection is taken over all primes $p$. Finally, define $R(N)$ to be the sum of all elements of $S$ not exceeding $N$. You are given that $R(20) = 18$ and $R(1000) = 2089$.

Find $R(10^7)$.

素数多叉树

一个完满$k$叉树是一棵具有单一根结点的树，其中每个结点要么是叶结点，要么恰好有$k$个有序子结点。$k$叉树的高度是从根结点到任一叶结点的最长路径上的边数。

例如，高度为$0$的完满$3$叉树有一棵，高度为$1$的完满$3$叉树有一棵，而高度为$2$的完满$3$叉树有七棵，如下图所示：

对于整数$n\ge 0$和$k\ge 2$，定义$t_k(n)$为高度不超过$n$的完满$k$叉树的数量。

因此，$t_3(0) = 1$，$t_3(1) = 2$，$t_3(2) = 9$。同时，$t_2(0) = 1$，$t_2(1) = 2$，$t_2(2) = 5$。

定义$S_k$为能整除任意整数$n\ge 0$对应的$t_k(n)$的正整数$m$的集合。例如，从上面的例子可知，$1$、$2$和$5$属于$S_2$，而$1$、$2$、$3$和$9$属于$S_3$。

记$S = \bigcap_p S_p$，其中交集取遍所有素数$p$。再定义$R(N)$为$S$中不超过$N$的所有元素之和。已知$R(20) = 18$，$R(1000) = 2089$。

求$R(10^7)$。

译注：原文的Full $k$-ary Tree直译为“满$k$叉树”；然而，在中文网络中，“满二叉树”的概念其实对应于英文中的Perfect Binary Tree，或“完美二叉树”。为示区别，这里参考网络资料将其翻译为“完满$k$叉树”。