---

Problem 931

---

Totient Graph

For a positive integer $n$ construct a graph using all the divisors of $n$ as the vertices. An edge is drawn between $a$ and $b$ if $a$ is divisible by $b$ and $a/b$ is prime, and is given weight $\phi(a)-\phi(b)$, where $\phi$ is the Euler totient function.

Define $t(n)$ to be the total weight of this graph.

The example below shows that $t(45) = 52$:

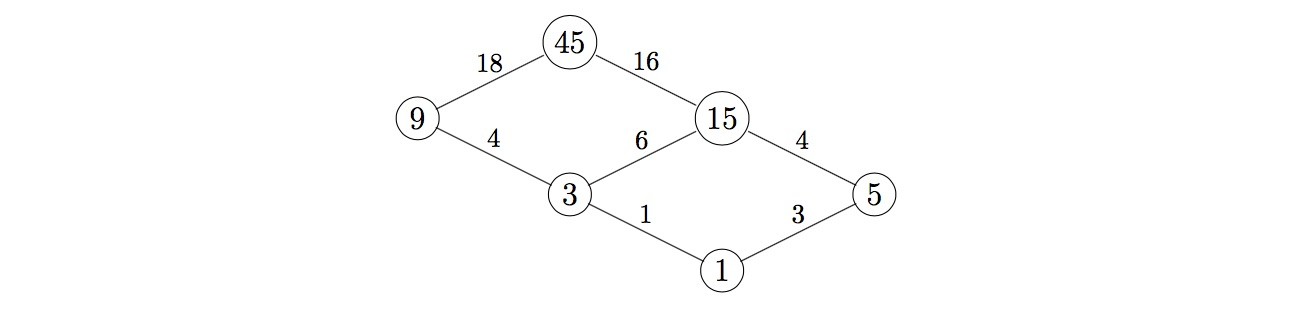
Let $T(N)=\displaystyle\sum_{n=1}^{N} t(n)$. You are given $T(10)=26$ and $T(10^2)=5282$.

Find $T(10^{12})$. Give your answer modulo $715827883$.

---

欧拉函数图

对于正整数$n$，以$n$的所有因数为顶点构造图。若$a$能被$b$整除，且$a/b$是素数，则在$a$和$b$对应的顶点之间作一条边，该边的权重为$\phi(a)-\phi(b)$，其中$\phi$表示欧拉函数。

定义$t(n)$为该图的总权重。

下图展示了$t(45) = 52$：

令$T(N)=\displaystyle\sum_{n=1}^{N} t(n)$。已知$T(10)=26$，$T(10^2)=5282$。

求$T(10^{12})$，并对$715827883$取余作为你的答案。

---