Problem 935

Rolling Square

A square of side length $b<1$ is rolling around the inside of a larger square of side length $1$, always touching the larger square but without sliding.

Initially the two squares share a common corner. At each step, the small square rotates clockwise about a corner that touches the large square, until another of its corners touches the large square. Here is an illustration of the first three steps for $b = \frac{5}{13}$.

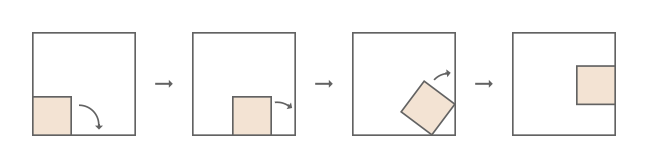
For some values of $b$, the small square may return to its initial position after several steps. For example, when $b = \frac{1}{2}$, this happens in $4$ steps; and for $b = \frac{5}{13}$ it happens in $24$ steps.

Let $F(N)$ be the number of different values of $b$ for which the small square first returns to its initial position within at most $N$ steps. For example, $F(6) = 4$, with the corresponding $b$ values:
$$\frac{1}{2},\quad 2 - \sqrt{2},\quad 2 + \sqrt{2} - \sqrt{2 + 4\sqrt{2}},\quad 8 - 5\sqrt{2} + 4\sqrt{3} - 3\sqrt{6},$$
the first three in $4$ steps and the last one in $6$ steps. Note that it does not matter whether the small square returns to its original orientation.
Also $F(100) = 805$.

Find $F(10^8)$.

翻滚的正方形

一个边长为$b<1$的小正方形在边长为$1$的大正方形内部以始终接触大正方形且不滑动的方式翻滚。

一开始，这两个正方形在一个角上重合。此后每一步，小正方形围绕其接触大正方形的一个角顺时针旋转，直到它的另一个角接触到大正方形。如下图所示是$b = \frac{5}{13}$时前三步的示意图。

对于$b$的某些取值，小正方形可能在若干步后回到其初始位置。例如，当$b = \frac{1}{2}$时，需要$4$步；而对于$b = \frac{5}{13}$，则需要$24$步。

令$F(N)$为使小正方形在最多$N$步内首次回到其初始位置的$b$的不同取值的数目。例如，$F(6) = 4$，对应的 $b$ 值为：
$$\frac{1}{2},\quad 2 - \sqrt{2},\quad 2 + \sqrt{2} - \sqrt{2 + 4\sqrt{2}},\quad 8 - 5\sqrt{2} + 4\sqrt{3} - 3\sqrt{6},$$
其中，前三个需要$4$步，最后一个需要$6$步。注意这里并不要求小正方形回到其初始方向。
此外，$F(100) = 805$。

求$F(10^8)$。