---

Problem 936

---

Peerless Trees

A peerless tree is a tree with no edge between two vertices of the same degree. Let $P(n)$ be the number of peerless trees on $n$ unlabelled vertices.

There are six of these trees on seven unlabelled vertices, $P(7)=6$, shown below.

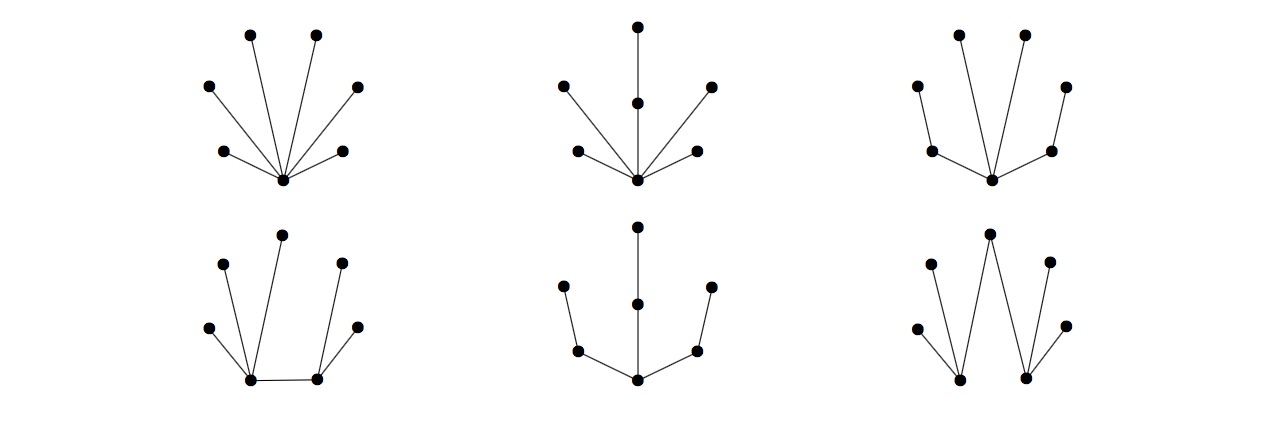
Define $\displaystyle S(N) = \sum_{n=3}^N P(n)$. You are given $S(10) = 74$.

Find $S(50)$.

---

无同树

无同树是指没有连接相同度数顶点的边的树。记$P(n)$为包含$n$个无标记顶点的无同树的数量。

包含七个无标记顶点的无同树有六棵，即$P(7)=6$，如下图所示。

定义$\displaystyle S(N) = \sum_{n=3}^N P(n)$。已知$S(10) = 74$。

求$S(50)$。

---