---

Problem 962

---

Angular Bisector and Tangent 2

Given is an integer sided triangle $ABC$ with $BC \le AC \le AB$.

$k$ is the angular bisector of angle $ACB$.

$m$ is the tangent at $C$ to the circumscribed circle of $ABC$.

$n$ is a line parallel to $m$ through $B$.

The intersection of $n$ and $k$ is called $E$.

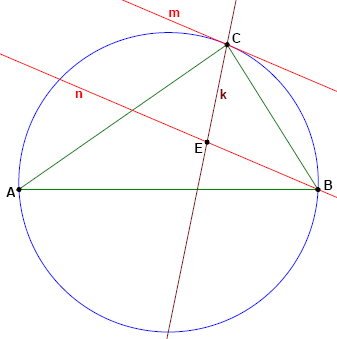
How many triangles $ABC$ with a perimeter not exceeding $1\ 000\ 000$ exist such that $CE$ has integral length?

Note: This problem is a more difficult version of Problem 296. Please pay close attention to the differences between the two statements.

---

角平分线与切线（二）

给定一个各边长均为整数且满足$BC \le AC \le AB$的三角形$ABC$：

$k$是角$ACB$的角平分线。

$m$是$ABC$外接圆在$C$点的切线。

$n$是过$B$点平行于$m$的直线。

$n$和$k$的交点记为$E$。

有多少个周长不超过$1\ 000\ 000$且$CE$的长度是整数的三角形$ABC$？

注：本题是第296题的更难版本；请特别注意两个问题陈述之间的差异。

---