Problem 155
Counting Capacitor Circuits
An electric circuit uses exclusively identical capacitors of the same value C.
The capacitors can be connected in series or in parallel to form sub-units, which can then be connected in series or in parallel with other capacitors or other sub-units to form larger sub-units, and so on up to a final circuit.
Using this simple procedure and up to n identical capacitors, we can make circuits having a range of different total capacitances. For example, using up to n=3 capacitors of 60μF each, we can obtain the following 7 distinct total capacitance values:
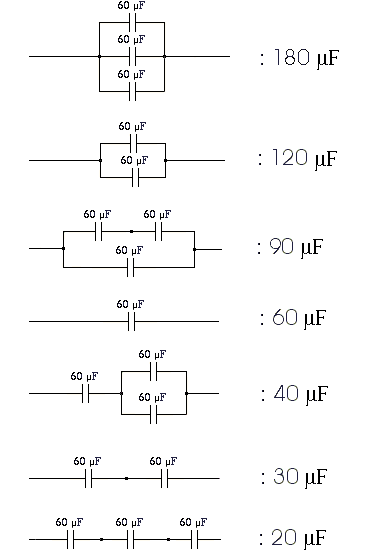
If we denote by D(n) the number of distinct total capacitance values we can obtain when using up to n equal-valued capacitors and the simple procedure described above, we have: D(1)=1, D(2)=3, D(3)=7 …
Find D(18).
Reminder : When connecting capacitors C1, C2 etc in parallel, the total capacitance is CT = C1 + C2 +…,
whereas when connecting them in series, the overall capacitance is given by:$\frac{1}{C_T}=\frac{1}{C_1}+\frac{1}{C_2}+…$.
电容电路计算
考虑如下电路,其中使用的电容都是完全相同的值C。
电容之间互相串联构成次级单元,然后次级单元之间互相串联或和其它次级单元或电容并联构成更大的次级单元,最终组成整个电路。
使用n个电容并重复这个简单的过程,我们可以构建出一系列总电容不同的电路。例如,使用最多n=3个值为60μF的电容,我们可以得到7种不同的总电容:

我们用D(n)表示当我们使用最多n个相同的电容并重复上述简单过程后,我们能够得到的总电容的种数,我们有:D(1)=1, D(2)=3, D(3)=7 …
求D(18)。
提醒:当电容C1,C2等等并联时,总电容为CT = C1 + C2 +…,
而当它们串联时,总电容为:$\frac{1}{C_T}=\frac{1}{C_1}+\frac{1}{C_2}+…$。