Problem 300
Protein folding
In a very simplified form, we can consider proteins as strings consisting of hydrophobic (H) and polar (P) elements, e.g. HHPPHHHPHHPH.
For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are 2n distinct proteins consisting of n elements.
When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous.
As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside.
Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
The figure below shows two possible ways that our example protein could be folded (H-H contact points are shown with red dots).
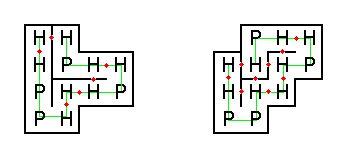
The folding on the left has only six H-H contact points, thus it would never occur naturally.
On the other hand, the folding on the right has nine H-H contact points, which is optimal for this string.
Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be 850 / 28=3.3203125.
What is the average number of H-H contact points in an optimal folding of a random protein string of length 15?
Give your answer using as many decimal places as necessary for an exact result.
蛋白质折叠
我们可以将蛋白质简单地想象成由疏水成分(H)和极性成分(P)构成的串,例如HHPPHHHPHHPH。
在这个问题中,蛋白质的方向是很重要的;例如,HPP和PPH被认为是不同的蛋白质。因此,有n个成分的不同蛋白质一共有2n种。
在自然界中,这些串一般都会折叠起来,使得H-H接触点尽可能多,因为这在能量上有优势。
结果是,H成分倾向于聚集在中间部分,而P成分则留在外围。
天然蛋白质当然是在三个维度上折叠的,但我们只考虑蛋白质在二维进行折叠的情况。
下图中展示了上述样例蛋白质两种可能的折叠方式(H-H接触点用红色点表示)。

左边的折叠方式只有6个H-H接触点,因此它不可能自然生成。
相反地,右边的折叠方式有9个H-H接触点,是这个样例蛋白质的最优折叠方式。
假定H成分和P成分在串的任何位置都等可能出现,对于一个长度为8的蛋白质串,最优折叠方式中H-H接触点的平均数目是850 / 28=3.3203125。
对于一个长度为15的蛋白质串,最优折叠方式中H-H接触点的平均数目是多少?
使用所必需的全部小数位,给出精确答案。
Gitalking ...