Problem 569
Prime Mountain Range
A mountain range consists of a line of mountains with slopes of exactly 45°, and heights governed by the prime numbers, pn. The up-slope of the kth mountain is of height p2k−1, and the downslope is p2k. The first few foot-hills of this range are illustrated below.
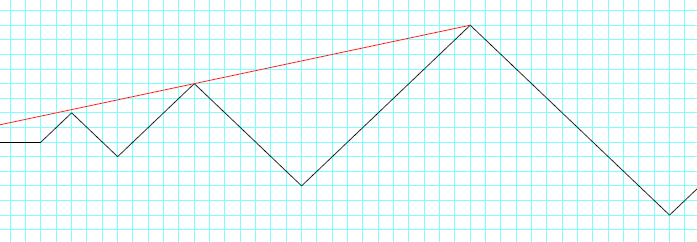
Tenzing sets out to climb each one in turn, starting from the lowest. At the top of each peak, he looks back and counts how many of the previous peaks he can see. In the example above, the eye-line from the third mountain is drawn in red, showing that he can only see the peak of the second mountain from this viewpoint. Similarly, from the 9th mountain, he can see three peaks, those of the 5th, 7th and 8th mountain.
Let P(k) be the number of peaks that are visible looking back from the kth mountain. Hence P(3)=1 and P(9)=3.
Also $\displaystyle \sum_{k=1}^{100} P(k) = 227$.
Find $\displaystyle \sum_{k=1}^{2500000} P(k)$.
素数山脉
一座山脉由一系列坡度为45度,高度与素数pn有关的山峰组成。第k座山峰的上行部分高度为p2k−1,下行部分高度为p2k,前几座山峰(准确地说只是山坡)如下图所示。

丹增打算从最矮的山峰开始攀登每一座山峰。每当他爬到一座山峰的峰顶时,他都会回头数一下此时能够看到多少座之前的山峰的峰顶。如上图,从第三座山峰的峰顶往回看的视线用红色标示,可见在他所处的位置只能看到第二座山峰的峰顶。类似地,从第9座山峰的峰顶往回看,他可以看到三座山峰的峰顶,分别是第5座、第7座和第8座。
记P(k)为从第k座山峰的峰顶往回看能够看见的峰顶数量。因此P(3)=1以及P(9)=3。
此外,$\displaystyle \sum_{k=1}^{100} P(k) = 227$。
求$\displaystyle \sum_{k=1}^{2500000} P(k)$。