---

Problem 577

---

Counting hexagons

An equilateral triangle with integer side length $n \ge 3$ is divided into $n^2$ equilateral triangles with side length 1 as shown in the diagram below.
The vertices of these triangles constitute a triangular lattice with $\frac{(n+1)(n+2)} 2$ lattice points.

Let $H(n)$ be the number of all regular hexagons that can be found by connecting 6 of these points.

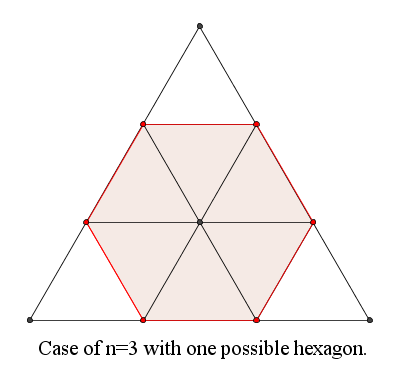
For example, $H(3)=1$, $H(6)=12$ and $H(20)=966$.

Find $\displaystyle \sum_{n=3}^{12345} H(n)$.

---

数六边形

边长为整数$n \ge 3$的等边三角形可以被分成$n^2$个边长为1的小等边三角形，如下图所示。
这些小三角形的$\frac{(n+1)(n+2)} 2$个顶点构成了一个三角形的格阵。

记$H(n)$为从这些顶点中取6个点构成的正六边形的数目。

当$n=3$时只有一个六边形

例如，$H(3)=1$，$H(6)=12$，而$H(20)=966$。

求$\displaystyle \sum_{n=3}^{12345} H(n)$。

---