---

Problem 587

---

Concave triangle

A square is drawn around a circle as shown in the diagram below on the left.
We shall call the blue shaded region the L-section.
A line is drawn from the bottom left of the square to the top right as shown in the diagram on the right.
We shall call the orange shaded region a concave triangle.

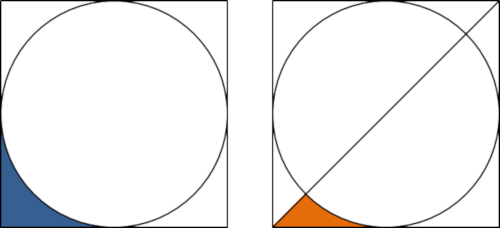
It should be clear that the concave triangle occupies exactly half of the L-section.

Two circles are placed next to each other horizontally, a rectangle is drawn around both circles, and a line is drawn from the bottom left to the top right as shown in the diagram below.

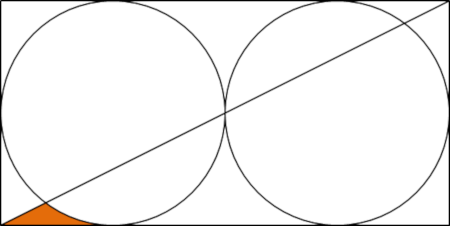
This time the concave triangle occupies approximately 36.46% of the L-section.

If $n$ circles are placed next to each other horizontally, a rectangle is drawn around the $n$ circles, and a line is drawn from the bottom left to the top right, then it can be shown that the least value of $n$ for which the concave triangle occupies less than 10% of the L-section is $n$ = 15.

What is the least value of $n$ for which the concave triangle occupies less than 0.1% of the L-section?

---

凹三角形

如下图左所示，在一个圆外作外接正方形。
我们称蓝色阴影区域为L型块。
如下图右所示，从正方形的左下角向右上角画一条直线。
我们称橙色阴影区域为凹三角形。

显然此时凹三角形的面积是L型块的一半。

如下图所示，将两个圆水平并排摆放，并作一个外接长方形，并从左下角向右上角画一条直线。

此时凹三角形的面积是L型块的约36.46%。

将$n$个圆水平并排摆放，并作一个外接长方形，并从左下角向右上角画一条直线，可以计算得出，使得此时凹三角形面积少于L型块的10%的最小的$n$=15。

使得凹三角形面积少于L型块的0.1%的最小的$n$值是多少？

---