Problem 594

Rhombus Tilings

For a polygon $P$ , let $t (P)$ be the number of ways in which $P$ can be tiled using rhombi and squares with edge length 1. Distinct rotations and reflections are counted as separate tilings.

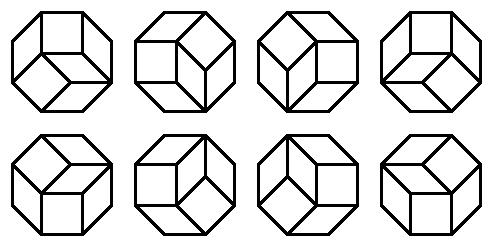
For example, if $O$ is a regular octagon with edge length 1, then $t (O) = 8$ . As it happens, all these 8 tilings are rotations of one another:

Let $O_{a, b}$ be the equal-angled convex octagon whose edges alternate in length between $a$ and $b$ .
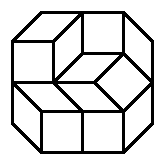
For example, here is $O_{2, 1}$ , with one of its tilings:

You are given that $t (O_{1, 1}) = 8$ , $t (O_{2, 1}) = 76$ and $t (O_{3, 2}) = 456572$ .

Find $t (O_{4, 2})$ .

菱形地砖

对于多边形 $P$ ，记 $t (P)$ 为用边长为1的菱形和正方形地砖铺满 $P$ 的方法数。旋转和翻转后相同的铺法视为不同的铺法。

例如，如果用 $O$ 表示一个边长为1的正八边形，那么 $t (O) = 8$ 。事实上，这8种铺法都可以通过旋转相互得到：

用 $O_{a, b}$ 表示边长交替为 $a$ 和 $b$ 的等角凸八边形。
例如，如下是 $O_{2, 1}$ 和其中一种铺法：

已知 $t (O_{1, 1}) = 8$ ， $t (O_{2, 1}) = 76$ ，以及 $t (O_{3, 2}) = 456572$ 。

求 $t (O_{4, 2})$ 。