Problem 604

Convex path in square

Let $F(N)$ be the maximum number of lattice points in an axis-aligned $N\times N$ square that the graph of a single strictly convex increasing function can pass through.

You are given that $F(1) = 2$, $F(3) = 3$, $F(9) = 6$, $F(11) = 7$, $F(100) = 30$ and $F(50000) = 1898$.
Below is the graph of a function reaching the maximum 3 for $N=3$:

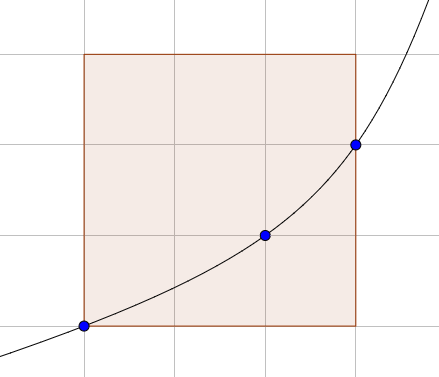
Find $F(10^{18})$.

正方形中的凹路径

记$F(N)$为，在一个和坐标系对齐的$N\times N$正方形中，一个严格凹单调增函数所能够穿过的格点数目最大值。

已知$F(1) = 2$，$F(3) = 3$，$F(9) = 6$，$F(11) = 7$，$F(100) = 30$以及$F(50000) = 1898$。
以下是$N=3$时达成最大值的函数图象：

求$F(10^{18})$。