---

Problem 707

---

Lights Out

Consider a $w\times h$ grid. A cell is either ON or OFF. When a cell is selected, that cell and all cells connected to that cell by an edge are toggled on-off, off-on. See the diagram for the $3$ cases of selecting a corner cell, an edge cell or central cell in a grid that has all cells on (white).

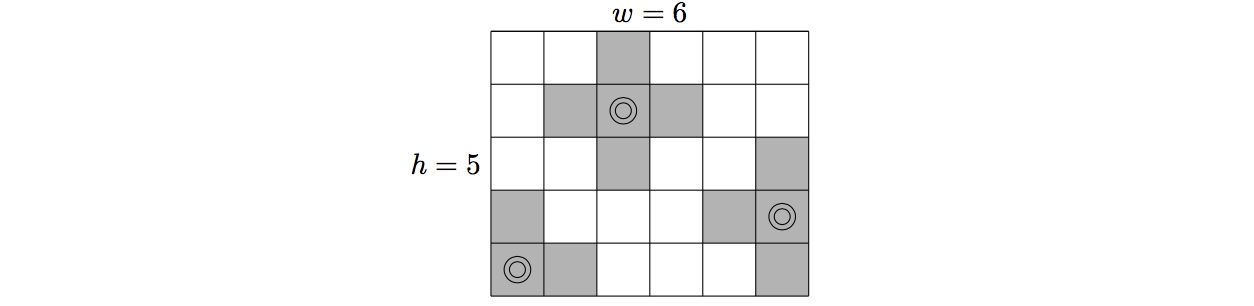
The goal is to get every cell to be off simultaneously. This is not possible for all starting states. A state is solvable if, by a process of selecting cells, the goal can be achieved.

Let $F(w,h)$ be the number of solvable states for a $w\times h$ grid. You are given $F(1,2)=2$, $F(3,3) = 512$, $F(4,4) = 4096$ and $F(7,11) \equiv 270016253 \pmod{1\ 000\ 000\ 007}$.

Let $f_1=f_2 = 1$ and $f_n=f_{n-1}+f_{n-2}, n \ge 3$ be the Fibonacci sequence and define
$$ S(w,n) = \sum_{k=1}^n F(w,f_k)$$
You are given $S(3,3) = 32$, $S(4,5) = 1052960$ and $S(5,7) \equiv 346547294 \pmod{1\ 000\ 000\ 007}$.

Find $S(199,199)$. Give your answer modulo $1\ 000\ 000\ 007$.

---

关灯

考虑一个$w\times h$的格阵，其中每一格有开或关两种状态。当某一格被选中时，这一格以及相邻格的状态会发生变化，若原本是开则变为关，若原本是关则变为开。下图展示了原本所有格均为开状态（表示为白色）的格阵在选中了一个角上的格、一个边上的格和一个中间的格后的情景。

从任意起始状态出发，并不是总能够将所有格变为关状态。如果能够做到，则称相应的起始状态为可解的。

记$F(w,h)$为$w\times h$格阵下可解起始状态的数目。已知$F(1,2)=2$，$F(3,3) = 512$，$F(4,4) = 4096$，$F(7,11) \equiv 270016253 \pmod{1\ 000\ 000\ 007}$。

考虑斐波那契数列$f_1=f_2 = 1$，$f_n=f_{n-1}+f_{n-2}, n \ge 3$，并记
$$ S(w,n) = \sum_{k=1}^n F(w,f_k)$$
已知$S(3,3) = 32$，$S(4,5) = 1052960$，$S(5,7) \equiv 346547294 \pmod{1\ 000\ 000\ 007}$。

求$S(199,199)$，并将你的答案对$1\ 000\ 000\ 007$取余。

---