Problem 716
Grid Graphs
Consider a directed graph made from an orthogonal lattice of $H\times W$ nodes. The edges are the horizontal and vertical connections between adjacent nodes. $W$ vertical directed lines are drawn and all the edges on these lines inherit that direction. Similarly, $H$ horizontal directed lines are drawn and all the edges on these lines inherit that direction.
Two nodes, $A$ and $B$ in a directed graph, are strongly connected if there is both a path, along the directed edges, from $A$ to $B$ as well as from $B$ to $A$. Note that every node is strongly connected to itself.
A strongly connected component in a directed graph is a non-empty set $M$ of nodes satisfying the following two properties:
- All nodes in $M$ are strongly connected to each other.
- $M$ is maximal, in the sense that no node in $M$ is strongly connected to any node outside of $M$.
There are $2^H\times 2^W$ ways of drawing the directed lines. Each way gives a directed graph $\mathcal{G}$. We define $S(\mathcal{G})$ to be the number of strongly connected components in $\mathcal{G}$.
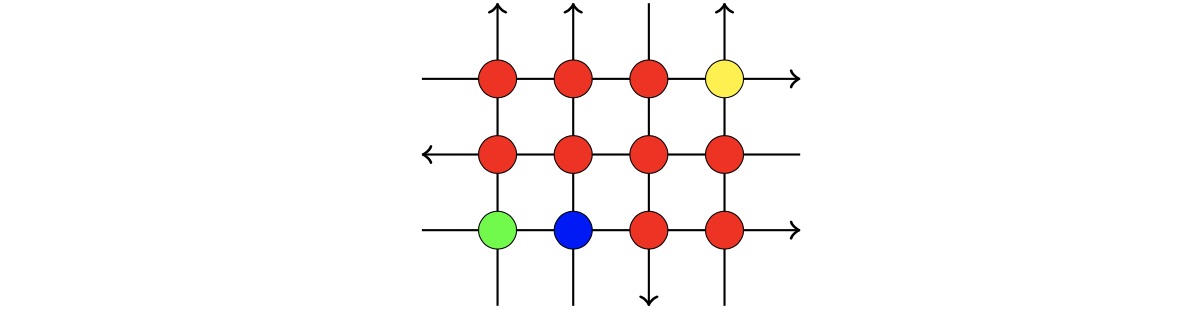
The illustration below shows a directed graph with $H=3$ and $W=4$ that consists of four different strongly connected components (indicated by the different colours).
Define $C(H,W)$ to be the sum of $S(\mathcal{G})$ for all possible graphs on a grid of $H\times W$. You are given $C(3,3) = 408$, $C(3,6) = 4696$ and $C(10,20) \equiv 988971143 \pmod{1\ 000\ 000\ 007}$.
Find $C(10\ 000,20\ 000)$ giving your answer modulo $1\ 000\ 000\ 007$.
格阵图
考虑一张基于$H\times W$个结点组成的格阵所构成的有向图,图中的边水平或竖直连接着相邻的结点。在格阵上可以画出$W$条竖直的有向直线,所有落在直线上的边和相应直线的方向一致;同理,在格阵上可以画出$H$条水平的有向直线,所有落在直线上的边和相应直线的方向也一致。
在有向图中,如果在两个结点$A$和$B$之间,存在一条沿着有向边由$A$到$B$的路径,同时也存在一条沿着有向边由$B$到$A$的路径,则称这两个结点是强连通的。注意每个结点和其自身都是强连通的。
有向图中的一个强连通分支是指满足以下两条性质的非空结点集$M$:
- $M$中的任意两个结点之间都是强连通的。
- $M$是极大的,这意味着不存在$M$之内的结点和$M$之外的结点之间是强连通的。
共有$2^H\times 2^W$种绘制有向直线的方式,每种方式确定了一张有向图$\mathcal{G}$。记$S(\mathcal{G})$为$\mathcal{G}$中强连通分支的数目。
下图展示了$H=3$、$W=4$时的一张有向图,这张图有四个不同的强连通分支(用不同颜色表示)。

记$C(H,W)$为所有基于$H\times W$的格阵的有向图对应$S(\mathcal{G})$之和。已知$C(3,3) = 408$,$C(3,6) = 4696$,$C(10,20) \equiv 988971143 \pmod{1\ 000\ 000\ 007}$。
求$C(10\ 000,20\ 000)$并将你的答案对$1\ 000\ 000\ 007$取余。