Problem 762

Amoebas in a 2D grid

Consider a two dimensional grid of squares. The grid has $4$ rows but infinitely many columns.

An amoeba in square $(x, y)$ can divide itself into two amoebas to occupy the squares $(x+1,y)$ and $(x+1,(y+1) \bmod 4)$, provided these squares are empty.

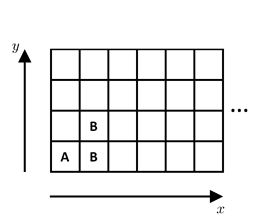
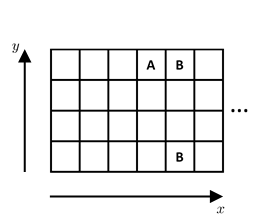
The following diagrams show two cases of an amoeba placed in square A of each grid. When it divides, it is replaced with two amoebas, one at each of the squares marked with B:

Originally there is only one amoeba in the square $(0, 0)$. After $N$ divisions there will be $N+1$ amoebas arranged in the grid. An arrangement may be reached in several different ways but it is only counted once. Let $C(N)$ be the number of different possible arrangements after $N$ divisions.

For example, $C(2) = 2$, $C(10) = 1301$, $C(20)=5895236$ and the last nine digits of $C(100)$ are $125923036$.

Find $C(100\ 000)$, enter the last nine digits as your answer.

二维格阵中的阿米巴原虫

考虑一个有$4$行、无穷列的二维格阵。

原本位于方格$(x,y)$中的一只阿米巴原虫，在目标方格没有被占据的情况下，可以将自身分裂成两只阿米巴原虫，并分别占据方格$(x+1,y)$和$(x+1,(y+1) \bmod 4)$。

在下图所示的两种情况中，一只阿米巴原虫原本位于方格A。在分裂为两只阿米巴原虫后，则分别占据了两个标记有B的方格：

一开始只有一只阿米巴原虫位于方格$(0, 0)$。经过$N$次分裂之后，格阵中将会分布有$N+1$只阿米巴原虫。不同的分裂顺序可能形成相同的分布情况，这些分布均算作相同的分布。记$C(N)$为经过$N$次分裂后所有可能的不同分布的总数。

例如，$C(2) = 2$，$C(10) = 1301$，$C(20)=5895236$，而$C(100)$的最后九位数字是$125923036$。

求$C(100\ 000)$，并将其最后九位数字作为你的答案。