---

Problem 777

---

Lissajous Curves

For coprime positive integers $a$ and $b$, let $C_{a,b}$ be the curve defined by:
$$
\begin{aligned}
x & = \cos \left(at\right) \\
y & = \cos \left(b\left(t-\frac{\pi}{10}\right)\right)
\end{aligned}
$$

where $t$ varies between $0$ and $2\pi$.

For example, the images below show $C_{2,5}$ (left) and $C_{7,4}$ (right):

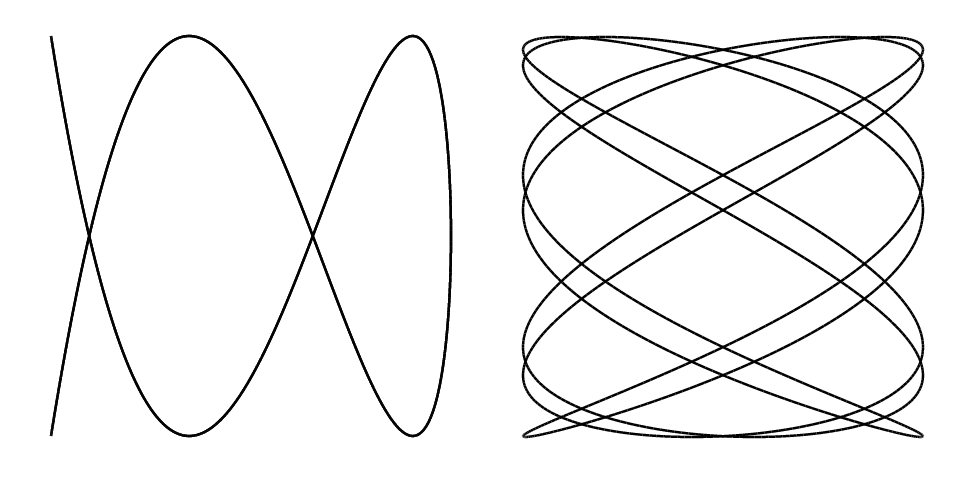
Define $d(a,b) = \sum (x^2 + y^2)$, where the sum is over all points $(x, y)$ at which $C_{a,b}$ crosses itself.

For example, in the case of $C_{2,5}$ illustrated above, the curve crosses itself at two points: $(0.31, 0)$ and $(-0.81, 0)$, rounding coordinates to two decimal places, yielding $d(2, 5)=0.75$. Some other examples are $d(2,3)=4.5$, $d(7,4)=39.5$, $d(7,5)=52$, and $d(10,7)=23.25$.

Let $s(m) = \sum d(a,b)$, where this sum is over all pairs of coprime integers $a,b$ with $2\le a\le m$ and $2\le b\le m$.
You are given that $s(10) = 1602.5$ and $s(100) = 24256505$.

Find $s(10^6)$. Give your answer in scientific notation rounded to $10$ significant digits; for example $s(100)$ would be given as $2.425650500e7$.

---

利萨茹曲线

对于互质的正整数$a$和$b$，记$C_{a,b}$为由如下参数方程定义的曲线：
$$
\begin{aligned}
x & = \cos \left(at\right) \\
y & = \cos \left(b\left(t-\frac{\pi}{10}\right)\right)
\end{aligned}
$$
其中参数$t$的取值范围是$0$到$2\pi$。

例如，下图所示分别是曲线$C_{2,5}$（左）和曲线$C_{7,4}$（右）：

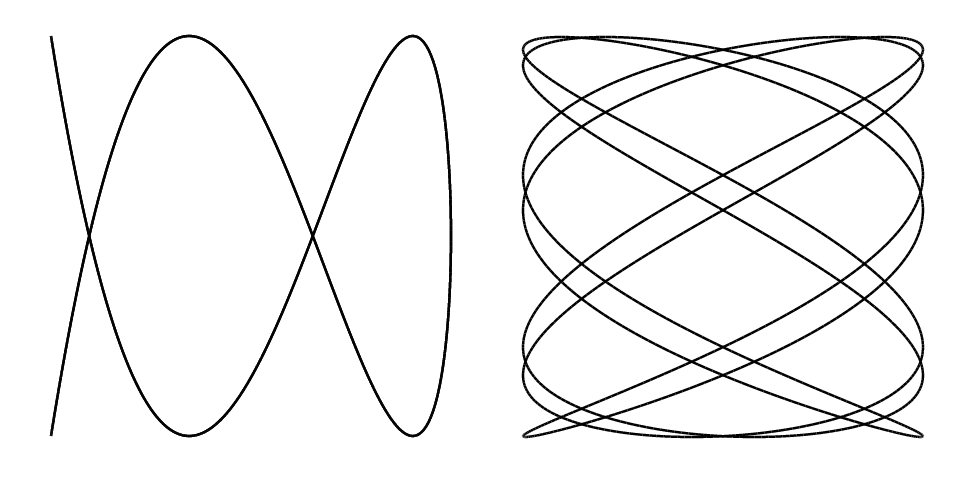
对于曲线$C_{a,b}$与自身相交产生的所有交点$(x,y)$，记$d(a,b) = \sum (x^2 + y^2)$。

例如，对于如上所示曲线$C_{2,5}$，其与自身相交产生两个交点：$(0.31, 0)$和$(-0.81, 0)$，均保留两位小数，因此$d(2, 5)=0.75$。此外，$d(2,3)=4.5$，$d(7,4)=39.5$，$d(7,5)=52$，$d(10,7)=23.25$。

对于所有满足$2\le a\le m$和$2\le b\le m$的互质整数对$a,b$，记$s(m) = \sum d(a,b)$。
已知$s(10) = 1602.5$，$s(100) = 24256505$。

求$s(10^6)$。将你的答案用科学计数法表示并保留$10$位有效数字；例如，$s(100)$应表示为$2.425650500e7$。

---