Problem 829

Integral Fusion

Given any integer $n>1$ a binary factor tree $T(n)$ is defined to be:

A tree with the single node $n$ when $n$ is prime.
A binary tree that has root node $n$, left subtree $T(a)$ and right subtree $T(b)$, when $n$ is not prime. Here $a$ and $b$ are positive integers such that $n = ab$, $a\le b$ and $b-a$ is the smallest.

For example $T(20)$:

We define $M(n)$ to be the smallest number that has a factor tree identical in shape to the factor tree for $n!!$, the double factorial of $n$.

For example, consider $9!! = 9\times 7\times 5\times 3\times 1 = 945$. The factor tree for $945$ is shown below together with the factor tree for $72$ which is the smallest number that has a factor tree of the same shape. Hence $M(9) = 72$.

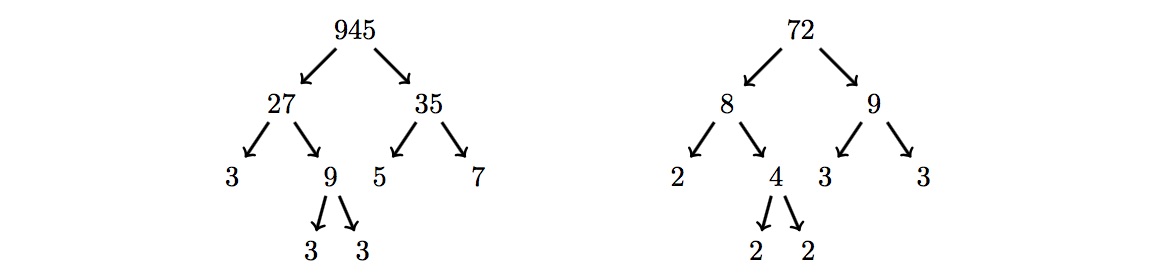
Find $\displaystyle\sum_{n=2}^{31} M(n)$.

整数合成

给定任意整数$n>1$，定义其对应的二叉因子树 $T(n)$如下：

若$n$是质数，则该树只有一个单独的结点$n$。
若$n$不是质数，则该树有根结点$n$、左子树$T(a)$和右子树$T(b)$，其中$a$和$b$都是正整数，且满足$n=ab$，$a\le b$，$b-a$取得最小值。

例如，$T(20)$如下图所示:

记$M(n)$为二叉因子树和$n!!$的二叉因子树形状相同的最小正整数，其中$n!!$表示$n$的双阶乘。

例如，$9!! = 9\times 7\times 5\times 3\times 1 = 945$。如下图所示，$945$和$72$的二叉因子树形状相同，且$72$是满足该条件的最小整数，因此$M(9) = 72$。

求$\displaystyle\sum_{n=2}^{31} M(n)$。