Problem 872

Recursive Tree

A sequence of rooted trees $T_{n}$ is constructed such that $T_{n}$ has $n$ nodes numbered $1$ to $n$ .

The sequence starts at $T_{1}$ , a tree with a single node as a root with the number $1$ .

For $n > 1$ , $T_{n}$ is constructed from $T_{n - 1}$ using the following procedure:

Trace a path from the root of $T_{n - 1}$ to a leaf by following the largest-numbered child at each node.
Remove all edges along the traced path, disconnecting all nodes along it from their parents.
Connect all orphaned nodes directly to a new node numbered $n$ , which becomes the root of $T_{n}$ .

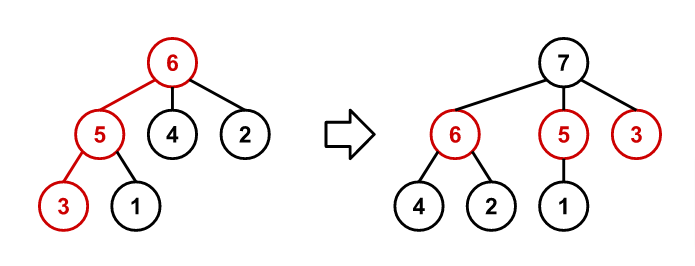
For example, the following figure shows $T_{6}$ and $T_{7}$ . The path traced through $T_{6}$ during the construction of $T_{7}$ is coloured red.

Let $f (n, k)$ be the sum of the node numbers along the path connecting the root of $T_{n}$ to the node $k$ , including the root and the node $k$ . For example, $f (6, 1) = 6 + 5 + 1 = 12$ and $f (10, 3) = 29$ .

Find $f (10^{17}, 9^{17})$ .

递归树

递归构造一个有根树序列 $T_{n}$ ，其中 $T_{n}$ 有 $n$ 个节点，编号分别为 $1$ 至 $n$ 。

序列的第一项为 $T_{1}$ ，这棵树只包含一个编号为 $1$ 的节点作为根节点。

对于 $n > 1$ ，树 $T_{n}$ 根据下列规则由 $T_{n - 1}$ 构造而成：

从 $T_{n - 1}$ 的根节点出发，不断沿编号最大的子节点移动，直至到达叶节点，并记录相应的路径。
移除路径上的所有边，使路径上的节点与其父节点分离。
将所有被分离出的节点连接到一个新的、编号为 $n$ 的节点，并将其作为 $T_{n}$ 的根节点。

例如，下图展示了 $T_{6}$ 和 $T_{7}$ 。 $T_{6}$ 中用于构造 $T_{7}$ 的路径被标示为红色。

记 $f (n, k)$ 为 $T_{n}$ 中连接根节点和编号为 $k$ 的节点的路径上，所有节点（包括路径的两端）的编号和。例如， $f (6, 1) = 6 + 5 + 1 = 12$ ， $f (10, 3) = 29$ 。

求 $f (10^{17}, 9^{17})$ 。